Considere o ciclo de Stirling, funcionando como refrigerador, para o qual as etapas são isotérmicas e as etapas são isovolumétricas. São conhecidas as temperaturas máximas e mínima e o razão entre o maior e o menor volume. Suponha que a substância de trabalho é um gás ideal com n moles e capacidade térmica molar a volume constante
(a) Esboce o diagrama correspondente a este ciclo, deixando claro cada uma das etapas.
(b) Determine o calor trocado e o trabalho realizado pelo gás em cada um dos quatro processos do ciclo.
(c) Qual a variação da entropia em cada ciclo?
Passo 1
a)
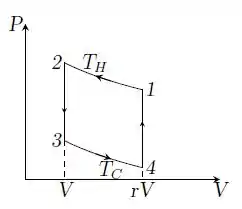
Passo 2
b) Processo isotérmico :
(a energia interna de um gás ideal depende apenas da temperatura), de modo que
Por tratar-se de um gás ideal, temos . Assim,
Processo isovolumétrico :
Processo isotérmico :
Analogamente ao processo , temos
Processo isovolumétrico :
Passo 3
c) Sendo uma função de estado, a variação da entropia em cada ciclo é zero.
Resposta
Ei, a resposta está no passo a passo :)