P2 de Física 2 da UFRJ - 2014.2

Marque a alternativa ERRADA a respeito do efeito Doppler.

1. Quando um observador se aproxima de uma fonte de onda em repouso, a frequência observada aumenta.
2. Quando uma fonte de onda se aproxima de um observador em repouso, a frequência observada aumenta.
3. Quando uma fonte de onda se aproxima de um observador em repouso, o número de onda observado aumenta.
4. Quando um observador se aproxima de uma fonte de onda em repouso, o comprimento de onda observado diminui.

Uma corda fixa nas duas extremidades e submetida a uma tensão oscila em seu terceiro modo normal, com comprimento de onda e . Se a tensão for quadruplicada, os novos e para este modo serão, respectivamente:

a): e .

b): e .

c): e .

d): e .

e) e .

Considere dois tubos de ar de mesmo comprimento e mesma seção transversal, um deles fechado numa das extremidades, e o outro, aberto em ambas, e ondas sonoras propagando-se nestes tubos. Considere as afirmações abaixo:

O deslocamento é máximo na extremidade do tubo aberto pois há um máximo de onda de pressão neste ponto.

O deslocamento é máximo na extremidade do tubo aberto pois há um nodo da onda de pressão neste ponto.

O comprimento de onda do modo fundamental, no tubo fechado, é o dobro do comprimento de onda deste modo no tubo aberto.

O comprimento de onda do modo fundamental, no tubo aberto, é o dobro do comprimento de onda deste modo no tubo fechado.

Qual(is) da(s) afirmação(ões) acima é(são) verdadeira(s)?

1. .
2. e .
3. e
4. e
5. e
6. e
7. e .

Considere um oscilador harmônico simples, inicialmente na posição de equilíbrio, e as três condições abaixo:

I -

II -

III -

Marque a alternativa correta:

1. Em todos os casos o corpo ficará sempre parado, pois já está na posição de equilíbrio.
2. O corpo atingirá o deslocamento máximo em menos tempo no caso .
3. O corpo atingirá o deslocamento máximo ao mesmo tempo nos casos e
4. O corpo oscilará com a mesma amplitude nos casos e .
5. A energia mecânica total do oscilador no caso é o dobro da do caso

Considere um corpo de massa , preso a uma mola ( de constante elástica e comprimento relaxado cuja outra extremidade presa está presa ao teto. Considere que pode oscilar, sem resistência, na vertical sob a ação de um campo gravitacional O corpo é solto, inicialmente em repouso, da posição em que a mola encontra-se relaxada.

1. DEDUZA a equação diferencial de movimento. Especifique CLARAMENTE o eixo e a origem de seu sistema de coordenadas.
2. Mostre que a equação diferencial de movimento pode ser escrita como a equação do oscilador harmônico simples em torno de uma nova posição de equilíbrio e determine esta posição.
3. Escreva a solução completa que descreve o movimento, em função dos dados do problema.

No momento em que começa a ser observada (, uma partícula de massa ligada a uma mola ideal de constante se afasta da origem e sua energia potencial vale metade da energia mecânica total. Sobre sua constante de fase podemos afirmar que:

Um oscilador levemente amortecido tem seu parâmetro de amortecimento muito menor que sua frequência natural Neste caso a energia mecânica média armazenada no oscilador num dado instante de tempo é dada por . A vida média destas oscilações é definida como o intervalo de tempo no qual a energia média se reduz de um fator . O número de oscilações que a partícula realiza neste intervalo pode ser expresso por:

Marque a alternativa ERRADA a respeito do comportamento de um pêndulo simples, na aproximação de pequenos ângulos.

1. Se dobrarmos o comprimento da corda do pêndulo, o seu período também vai dobrar.
2. O período não depende das condições iniciais.
3. A velocidade máxima de oscilação não depende do valor da massa do pêndulo.
4. Um mesmo pêndulo na lua oscila com menor frequência do que na terra sob as mesmas condições iniciais.

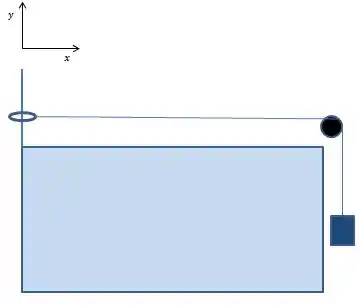
Uma corda homogênea e inextensível de comprimento e densidade linear de massa é tensionada por um bloco de massa , como mostrado na figura. A extremidade esquerda da corda está ligada a um anel de massa desprezível, o qual pode deslizar sem atrito em uma haste vertical. Considere o eixo apontado para direita com origem na posição do anel e suponha que ondas transversais sejam produzidas na corda usando-se uma fonte externa de frequência variável (não indicada na figura). Suponha conhecida a velocidade da onda nesta corda sob estas condições e que a corda não descole da roldana em nenhum momento.

1. Mostre que , onde e são constantes, é solução da equação de onda unidimensional(não é necessário deduzi-la) e determine a relação entre e .
2. Utilizando as condições de contorno e determine o comprimento de onda do n-ésimo modo normal de vibração.
3. Esboce os três modos normais de vibração de menor frequência observados na corda indicando explicitamente o comprimento de onda de cada um.

Duas balanças são constituídas, cada uma, por uma mola e um prato, em que se deposita uma massa a ser medida. Observa-se que para a primeira balança, o prato não oscila, mas a balança demora um certo tempo para marcar o valor correto depois que a massa é posta no prato. Nota-se também que a segunda balança oscila várias vezes antes que o prato pare e esse valor possa ser lido. Assinale a alternativa INCORRETA:

1. Na primeira balança observa-se um regime de amortecimento crítico ou supercrítico.
2. Na segunda balança observa-se um regime de amortecimento subcrítico.
3. Quanto mais amortecido o sistema, menos tempo a balança leva para marcar o valor correto.
4. Se não houvesse nenhum tipo de amortecimento, a balança poderia oscilar por tempo indeterminado.
5. O valor da massa altera a frequência natural de oscilação do sistema massa+prato+mola.