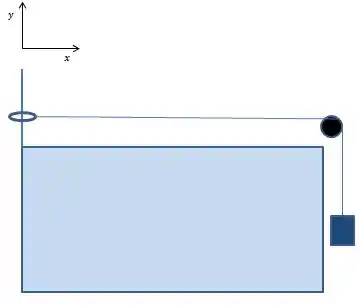
Uma corda homogênea e inextensível de comprimento e densidade linear de massa é tensionada por um bloco de massa , como mostrado na figura. A extremidade esquerda da corda está ligada a um anel de massa desprezível, o qual pode deslizar sem atrito em uma haste vertical. Considere o eixo apontado para direita com origem na posição do anel e suponha que ondas transversais sejam produzidas na corda usando-se uma fonte externa de frequência variável (não indicada na figura). Suponha conhecida a velocidade da onda nesta corda sob estas condições e que a corda não descole da roldana em nenhum momento.
- Mostre que , onde e são constantes, é solução da equação de onda unidimensional(não é necessário deduzi-la) e determine a relação entre e .
- Utilizando as condições de contorno e determine o comprimento de onda do n-ésimo modo normal de vibração.
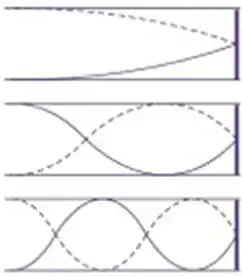
- Esboce os três modos normais de vibração de menor frequência observados na corda indicando explicitamente o comprimento de onda de cada um.
Passo 1
a):
A ideia desse item é simples: Vamos aplicar essa equação na equação de onda unidimensional. Se tudo der certo, beleza. A equação de onda unidimensional é:
Logo, provar que a equação do enunciado é uma solução dessa equação é provar que:
Onde .
Ok! Então é simples, vamos calcular as derivadas parciais de segunda ordem dali de cima e vê no que vai dar:
Onde ali a gente derivou só em relação ao . Derivando de novo:
Agora vamos fazer a segunda derivada parcial, agora em relação ao tempo:
Agora, lembrando que , podemos reescrever as equações como:
Logo, na equação principal:
Logo, como a função não pe igual a zero, a expressão acima só se anulará se :
Então provamos que é solução da equação de onda e que a relação entre e é essa acima.
Passo 2
b):
A primeira condição de contorno nos diz que a derivada parcial da função em relação à , quando aplicada em , nos dá um resultado igual à zero. Usando a expressão que a gente calculou um pouquinho antes:
Para
Então, reescrevendo
A segunda opção diz que
Então vamos aplicar na nova expressão:
Mas , nos diz que isso tem que valer pra qualquer instante . Ou seja, a expressão tem que se anular no ponto para qualquer tempo. Então, temos que dizer que o que anula a expressão é a parte que não depende do tempo, ou seja:
Só que não é igual a zero.(Porque o já é zero, se tivermos os dois igual a zero, a onda será nula).Então:
E quando isso acontece? Quando o ângulo ali do cosseno for um múltiplo ímpar de .(como . Então:
Estamos quase lá. Agora, usando a definição de número de onda:
Logo:
Pronto (:
Isso vale para
Passo 3
Por primeiro harmônico, vamos pegar o menor valor de . Então, , temos:
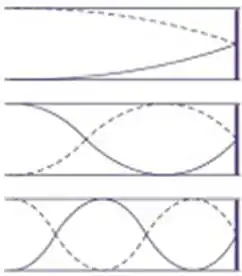
No primeiro caso, vamos desenhar um quarto de comprimento de onda. No segundo, meio comprimento de onda mais um quarto. E no terceiro, um comprimento de onda mais um quarto. Logo:
Resposta
a):
b):
c):