Considere dois tubos de ar de mesmo comprimento e mesma seção transversal, um deles fechado numa das extremidades, e o outro, aberto em ambas, e ondas sonoras propagando-se nestes tubos. Considere as afirmações abaixo:
O deslocamento é máximo na extremidade do tubo aberto pois há um máximo de onda de pressão neste ponto.
O deslocamento é máximo na extremidade do tubo aberto pois há um nodo da onda de pressão neste ponto.
O comprimento de onda do modo fundamental, no tubo fechado, é o dobro do comprimento de onda deste modo no tubo aberto.
O comprimento de onda do modo fundamental, no tubo aberto, é o dobro do comprimento de onda deste modo no tubo fechado.
Qual(is) da(s) afirmação(ões) acima é(são) verdadeira(s)?
- .
- e .
- e
- e
- e
- e
- e .
Passo 1
Lembrando-se dos padrões de deslocamento que aparecem nos tubos abertos e fechados(to falando disso aqui )
Aberto:
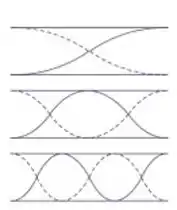
Fechado:
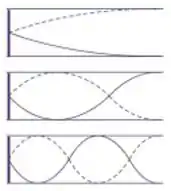
Passo 2
Vamos lá:
Nas extremidades dos tubos abertos não pode haver um máximo de pressão pelo seguinte motivo: Ali o ar que tá dentro do tubo, um ar com pressão oscilante, entra em contato com o ar da atmosfera, que tem uma pressão fixa. Então nas pontas dos tubos abertos existem, na verdade, nós de pressão.
Ai sim tá certo. Podemos ver isso com o padrão das ondas estacionárias nos tubos abertos e também por causa do lance da pressão fixa da atmosfera. Lembre-se de uma coisa: Onde tem nó de pressão tem máximo de deslocamento e vice-versa.
Passo 3
Pra um tubo aberto, temos que:
Modo fundamental implica em . Logo:
Para um tubo fechado, temos que:
No modo fundamental, :
Ou seja, realmente o comprimento é o dobro do tubo aberto.
Passo 4
: Acabamos de ver que não é o comprimento do aberto que é o dobro do fechado, e sim o contrário.
Logo, a resposta certa é:
g)
Resposta
g)