P3 de Física 2 da USP - 2018

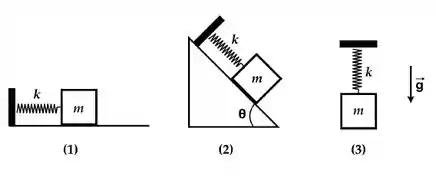
A figura mostra três osciladores harmônicos de mesma massa e constante elástica Não há atrito entre o bloco e as superfícies de contato, nem resistência do ar. Pode-se dizer das frequências angulares naturais de oscilação que

Uma certa onda transversal com amplitude e frequência transfere energia em uma corda a uma taxa média . Se a amplitude e a frequência são dobradas, a nova onda transferirá energia a uma taxa média de:

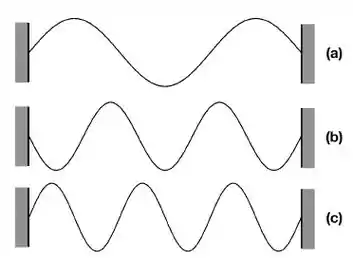
A figura mostra fotografias de diferentes modos de vibração de uma corda de de comprimento e densidade linear , presa por ambas as extremidades e submetida a uma tensão de . As frequências de oscilação transversal da corda para os três casos são

Uma corda de densidade linear de massa m = 50 g cm􀀀1 é esticada sob uma tensão de 720 N. A corda tem de comprimento e, em uma das extremidades, introduzem-se oscilações de frequência com amplitude . Depois de quanto tempo após o início das oscilações, a frente de onda atinge a outra extremidade da corda?

1. 3 s
2. 30 s
3. 0,3 s
4. 0,25 s
5. 2,5 s

Um sistema massa-mola não amortecido é formado por um bloco de massa e por uma mola de constante elástica O sistema é submetido a uma força externa dada por

sendo

Sabendo que no instante , o bloco encontra-se em repouso, na posição , é correto afirmar que:

a)

b)

c)

d)

e) Nenhuma das demais alternativas.

Uma cantoneira maciça é formada por duas barras delgadas idênticas, cada uma de massa M e comprimento L, conectadas perpendicularmente. Na junção entre as barras há um pequeno orifício circular de raio desprezível. O conjunto é pendurado por meio de um pino de suspensão passando pelo orifício e em torno do qual a cantoneira pode girar sem atrito, como mostrado na figura, numa situação em que o sistema está em equilíbrio.

Quando a cantoneira é deslocada ligeiramente para a direita ou para a esquerda, ela oscila no plano da figura

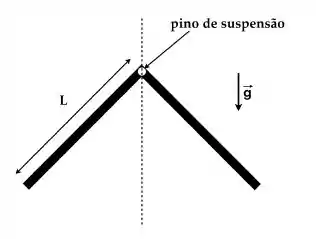
(a) Esboce o diagrama de forças externas que agem sobre a cantoneira num instante de tempo em que a linha que contém o CM desta faz um ângulo com a vertical.

(b) Adote um sistema de coordenadas com uma base de versores e determine o vetor torque total externo sobre a cantoneira na situação do item (a).

(c) No limite de pequenas oscilações, obtenha a equação diferencial para o ângulo , bem como a frequência natural das oscilações da cantoneira.

(d) Se o valor inicial para o ângulo é e a barra é liberada a partir do repouso, escreva a solução completa para o ângulo neste mesmo limite.

(e) Ainda no limite de pequenas oscilações, calcule as energias cinética e potencial da cantoneira como função do tempo. Verifique seu resultado, certificando-se de que a soma é constante. No limite de pequenos ângulos: