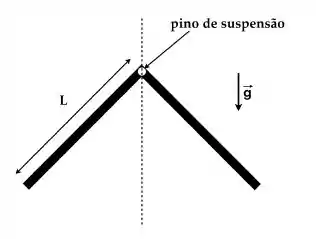
Uma cantoneira maciça é formada por duas barras delgadas idênticas, cada uma de massa M e comprimento L, conectadas perpendicularmente. Na junção entre as barras há um pequeno orifício circular de raio desprezível. O conjunto é pendurado por meio de um pino de suspensão passando pelo orifício e em torno do qual a cantoneira pode girar sem atrito, como mostrado na figura, numa situação em que o sistema está em equilíbrio.
Quando a cantoneira é deslocada ligeiramente para a direita ou para a esquerda, ela oscila no plano da figura
(a) Esboce o diagrama de forças externas que agem sobre a cantoneira num instante de tempo em que a linha que contém o CM desta faz um ângulo com a vertical.
(b) Adote um sistema de coordenadas com uma base de versores e determine o vetor torque total externo sobre a cantoneira na situação do item (a).
(c) No limite de pequenas oscilações, obtenha a equação diferencial para o ângulo , bem como a frequência natural das oscilações da cantoneira.
(d) Se o valor inicial para o ângulo é e a barra é liberada a partir do repouso, escreva a solução completa para o ângulo neste mesmo limite.
(e) Ainda no limite de pequenas oscilações, calcule as energias cinética e potencial da cantoneira como função do tempo. Verifique seu resultado, certificando-se de que a soma é constante. No limite de pequenos ângulos:
Passo 1
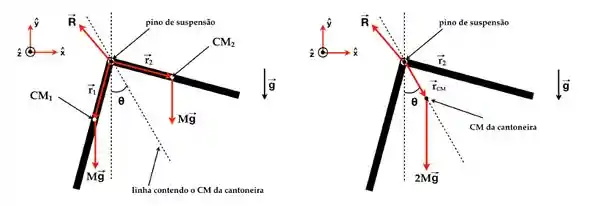
a) A figura abaixo mostra duas possíveis representações do diagrama de forças externas contendo: o peso de cada uma das barras da cantoneira aplicados aos seus respectivos ou o peso total da cantoneira aplicado no correspondente e a força de reação aplicada pelo pino de suspensão na cantoneira.
Passo 2
b) Tomaremos como ponto de referência para o cálculo do torque o ponto de suspensão (O), de forma que as únicas forças contribuindo para o torque são as forças peso. Logo
No sistema de coordenadas adotado temos que
Passo 3
c) De acordo com a 2a lei de Newton para rotações
De forma que no limite de pequenas oscilações , temos
Portanto
O momento de inércia da cantoneira com respeito a um eixo passando pelo ponto de suspensão O pode ser obtido por meio do teorema dos eixos paralelos
De forma que temos para a equação diferencial final
com
Passo 4
d) equação diferencial do item (c) é a do MHS, cuja solução geral é
e
Para as condições iniciais dadas
e
Como , temos que
Passo 5
e) A energia cinética devido a rotação em torno de O, com velocidade angular de é dada por
Para a energia potencial, tomaremos como ponto de referência o ponto de suspensão para calcular a altura CM da cantoneira. Na posição de equilíbrio, o CM da cantoneira esta a uma distância abaixo de O, de modo que quando o sistema girou um ângulo com respeito a vertical
Onde usou-se o limite de pequenas oscilações. Como a força de reação não realiza trabalho, a energia mecânica desse sistema deve se conservar.
Resposta
Ei, a resposta está no passo a passo :)