P2 de Física 2 da USP - 2019

O gráfico abaixo representa a posição de uma partícula em função do tempo , para um oscilador harmônico amortecido. A amplitude inicial , em , e a frequência angular em , desse oscilador são, respectivamente, dadas por:

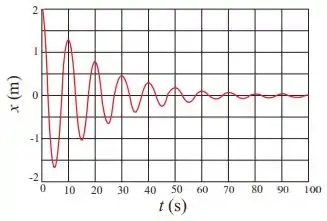
a) e .

b) e .

c) e .

d) e .

e) e .

Um sistema de suspensão mecânica ideal de massa e constante elas´tica oscila sem amortecimento, sujeito à força externa da forma . Um estudo demonstra que, quando o sistema atinge o regime estacionário, a amplitude de oscilação do sistema em função da frequência angular da força externa se comporta como na figura ao lado. O valor da constante elástica dos sitema de suspensão é:

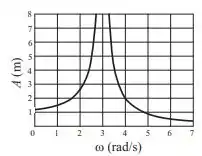
a) .

b) .

c) .

d) .

e) .

A amplitude de um osciladro harmônico com amortecimento subcrítico diminui de seu valor inicial, em . O valor do tempo característico de decaimento deste oscilador é:

a) .

b) .

c) .

d) .

e) .

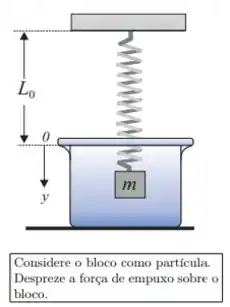
Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:

onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.

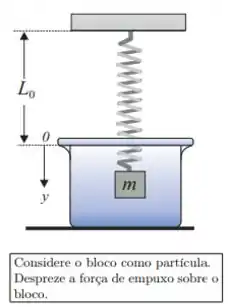
Q6) Determine a solução particular da equação diferencial não-homogênea.

Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:

onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.

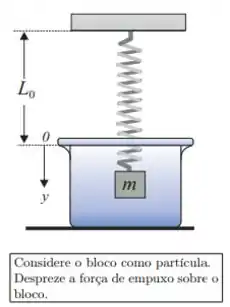
Q7) O movimento do oscilador descrito pela equação homogênea é crítico, subcrítico ou supercrítico? Justifique sua resposta numericamente.

Osciladores harmônicos amortecidos costumam ser modelados pela equação diferencial

Uma maneira de encontrar as soluções desta equação diferencial é assumir a função tentativa como solução e encontrar quais valores de que realmente a tornam solução da equação diferencial (1). Fazendo a substituição de em (1), vemos que os valores de que tornam a função tentativa solução de (1) são:

Os valores de levam a três soluções distintas, as quais são classificadas conforme o radicando presnete em e seja maior, igual ou menor que zero. Com base nestas informações, escolha a alternativa correta:

a) Todas as três soluções da equação diferencial (1) referentes aos radicandos maior, menor ou igual a zero modelam oscilações, porque toda exponencial de um número real real pode ser expressa em termos de funções periódicas, como senos e cossenos.

b) Na situação onde assume valores complexos, só a parte real de tem siginificado físico.

c) O caso onde corresponde ao único caso onde ocorrem oscilações porque podemos expressar como uma função periódica.

d) Se a frequência natural do sistema for muito maior que o fator dissipativo , a amplitude de oscilação vai aumentando conforme o tempo passa.

e) Quando , o oscilador retorna muito mais rapidamente para a posição de equilíbrio do que quando .

Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:

onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.

Q8) Uma vez que no instante a posição do bloco é e a sua velocidade , determine a solução geral . Resolva de forma literal, sem fazer substituições numéricas.

Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:

onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.

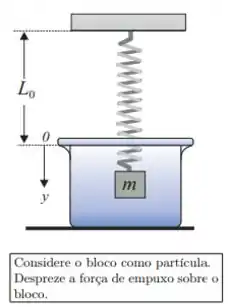
Q5) Escreva a equação diferencial que descreve o movimento deste oscilador, explicitando os valores numéricos dos coeficientes no sistema MKS.

Q6) Determine a solução particular da equação diferencial não-homogênea.

Q7) O movimento do oscilador descrito pela equação homogênea é crítico, subcrítico ou supercrítico? Justifique sua resposta numericamente.

Q8) Uma vez que no instante a posição do bloco é e a sua velocidade , determine a solução geral . Resolva de forma literal, sem fazer substituições numéricas.