P1 de Física 2 da USP - 2019

Os três gráficos da figura ao lado representam a posição em função do tempo, , de partículas realizando diferentes movimentos harmônicos simples, identificados pelas letras H, K e J. Se as velocidades máximas das partículas são dadas por , e para os movimentos H, K e J, respectivamente, e , e são as respectivas frequências angulares dos movimentos, podemos afirmar que:

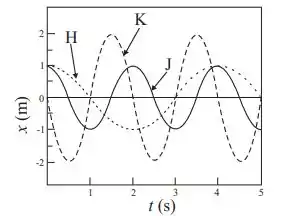
a) e .

b) e .

c) e .

d) e .

e) e .

Um malabarista de está pendurado por uma corda com constante elástica de , que pode ser modelada como uma mola. O malabarista, liberado quando a corda não está esticada, desce uma distância até parar. A amplitude de oscilação será:

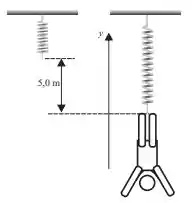
a)

b)

c)

d)

e)

Uma mola de constante elástica tem uma extremidade fixada numa parede e a outra, no centro de um disco de massa M, que pode movimentar-se numa superfície horizontal. No instante inicial, o disco está em repouso na posição de equilíbrio. A partir da posição de equilíbrio, o disco é puxado para a direita até que a elongação da mola seja . Depois de solto a partir da posição , o disco rola sem deslizar, realizando um movimento harmônico simples. A frequência angular do movimento é:

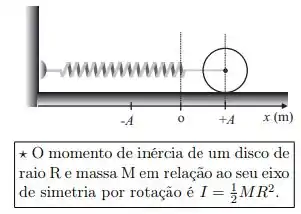
a)

b)

c)

d)

e)

Um pêndulo, constituído por um disco fino de massa e raio , e centro de massa em C, é pendurado por um ponto a uma eixo fixo, conforme mostra a figura. O disco pode balançar livremente, de um lado para outro, quando é deslocado, de um ângulo , a partir de sua posição de equilíbrio. Se o movimento do pêndulo é restringido a ângulos pequenos, e a distância entre o ponto de suspensão e o centro de massa é , o período das oscilações quando ele oscila em torno do ponto é:

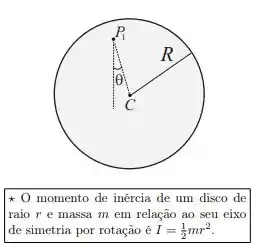
a)

b)

c)

d)

e)

O gráfico mostra a velocidade em função do tempo de uma partícula de massa , ligada a uma mola, que move-se em movimento retilíneo sobre uma mesa horizontal sem atrito, realizando um MHS. A velocidade inicial da partícula é . A expressão do deslocamento da partícula em função do tempo é:

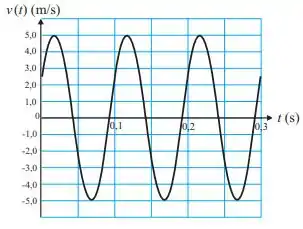
a)

b)

c)

d)

e)

Uma mola tem uma extremidade fixada numa parede e a outra num carrinho, que pode movimentar-se numa superfície horizontal sem atrito. O carrinho me movimento comporta-se como um oscilador harmônico realizando um movimento harmônico simples. Se o carrinho realiza ciclos/s e no instante inicial de movimento encontra-se na posição com velocidade , a amplitude da oscilação é:

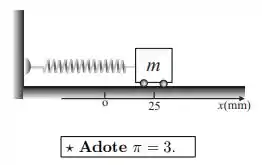
a)

b)

c)

d)

e)

Um malabarista de está pendurado por uma corda com constante elástica de , que pode ser modelada como uma mola. Ele é puxado para baixo, até um ponto em que a corda está mais comprida do que seu comprimento não esticado, e depois é liberado a partir desta posição. Adotando o eixo mostrado na figura e considerando que as oscilações verticais do malabarista constituem um MHS unidimensional, a posição do malabarista como função do tempo, medida a partir da posição de equilíbrio do malabarista, é:

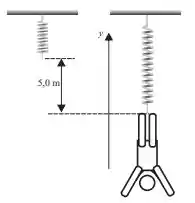
a)

b)

c)

d)

e)

A figura ao lado é o diagrama de energia potencial para uma trajetória de massa , que está sujeita à força conservativa , onde . A partícula é liberada do repouso na posição , com energia mecânica total , represnetada na figura por uma linha horizontal tracejada. Com base nestas informações podemos afirmar que a equação horária que descreve a velocidade da partícula em , é:

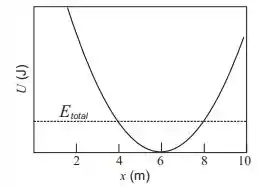
a)

b)

c)

d)

e)