P3 de Física 2 da USP - 2014

Dois pêndulos, cada um composto por um fio de comprimento prendendo uma partícula de massa , realizam um movimento harmônico simples (pequenas amplitudes) com uma mola de constante elástica e massa desprezível unindo as massas no plano de oscilação. Quais o modos normais de oscilação?

1. e
2. e
3. e
4. e
5. e

Um objeto de preso a uma mola, oscila sem atrito sujeito a uma força , conhecendo a constante elástica da mola, , obtenha o período e a amplitude do movimento.

Uma cadeia linear de partículas de massa , ligadas com molas de constante elástica e massa desprezível, precisa de quantas condições iniciais para a completa descrição do sistema? Considere apenas deslocamentos longitudinais.

Considerando o oscilador harmônico forçado não-amortecido no regime de ressonância (), que parte do repouso na posição de equilíbrio, qual o perfil da curva que passa pelos pontos de máximo da oscilação?

1. Linear decrescente
2. Exponencial decrescente
3. Constante
4. Linear crescente
5. Exponencial crescente

Considere o oscilador harmônico amortecido descrito pela equação diferencial

Qual a potência média fornecida pela força externa em uma oscilação?

Considere um oscilador harmônico não-amortecido na presença da força externa . Qual a solução geral para no regime de ressonância () sabendo que o oscilador se encontra inicialmente em repouso e na origem?

Dado um sistema de duas partículas de massa ligados por três molas de constante elástica e massa desprezível, como ilustrado abaixo:

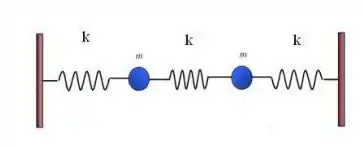
O sistema possui dois modos normais de vibração, e , onde . Quando o sistema oscila com frequência ou , a frequência de oscilação do centro de massa é respectivamente

1. e
2. e
3. e
4. e
5. e

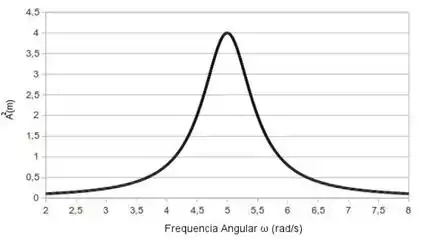
O gráfico abaixo mostra o quadrado da amplitude, , em função da frequência de oscilação de uma força senoidal aplicada. Dado que o sistema é fracamente amortecido, obtenha seu fator de qualidade, .

Um corpo de oscila preso a uma mola que tem constante elástica igual a . A constante de amortecimento linear vale . O sistema é excitado por uma força senoidal de valor máximo igual a e frequência angular de . Qual é a amplitude das oscilações?

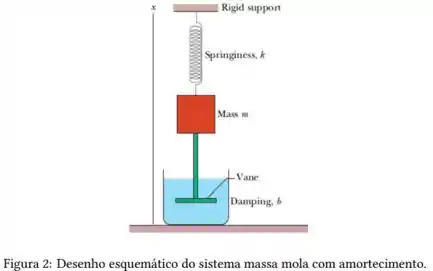
Considere a equação da amplitude de oscilação do sistema mostrado na figura abaixo,

Onde é a amplitude constante de uma força oscilatória externa de frequência . Qual é a amplitude de oscilação e a velocidade máxima do objeto quando excitado na frequência de ressonância?

1. e
2. e
3. e
4. e
5. e

Um circuito eletrônico é formado por uma resistência elétrica, , por uma indutância, , por um capacitor, e por uma fonte alternada . A equação diferencial para a corrente elétrica, é

o que se mostra que o circuito se comporta como um oscilador harmônico forçado e amortecido.

1. Qual a frequência angular natural de oscilação da corrente, e o parâmetro de amortecimento, ?
2. Sendo

a solução estacionária, determine faça um esboço do gráfico de em função de .

3. Para , escreva a solução geral da equação diferencial dada acima.
4. Se as condições iniciais são e , determine a solução específica para este oscilador.