P1 de Física 2 da USP - 2016

A figura mostra os gráficos da energia cinética K em função da posição x para três osciladores harmônicos do tipo bloco-mola que têm a mesma massa e que descrevem movimentos harmônicos simples. Pode-se dizer que:

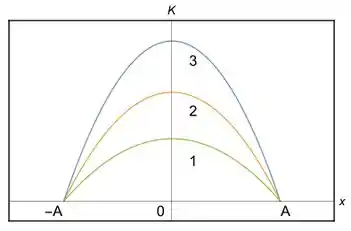
(a) A constante elástica do oscilador 2 é maior que a do oscilador 3.

(b) O período de oscilação associado ao oscilador 1 é menor que aquele dos osciladores 2 e 3.

(c) O oscilador 3 completa uma oscilação em um tempo menor que os outros dois.

(d) A constante elástica do oscilador 3 é maior que a dos osciladores 1 e 2, sendo a constante elástica do oscilador 2 menor que a do oscilador 1.

(e) Os três osciladores tem a mesma freqüência de oscilação.

Um bloco de massa m está conectado a uma mola de constante elástica em um plano inclinado que forma um ângulo em relação à horizontal. No instante , o bloco é solto da posição , com velocidade inicial nula. Considerando que a mola está relaxada (nem comprimida, nem esticada) quando , determine:

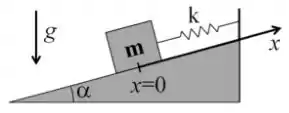
(a) A equação do movimento do bloco ao longo do eixo x mostrado na figura.

(b) A posição da massa em função do tempo. Qual é a amplitude do movimento e os valores máximo () e mínimo ( de ?

(c) A energia cinética em função do tempo.

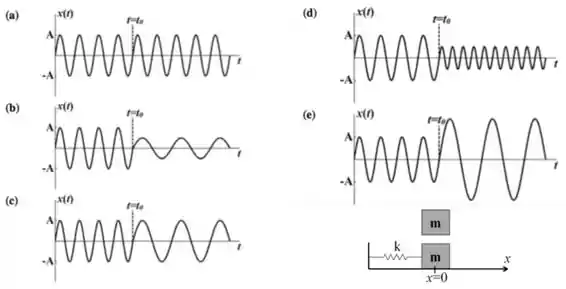
Um oscilador harmônico simples constituído por um bloco de massa m e uma mola de constante elástica realiza um movimento periódico com amplitude em torno da posição de equilíbrio . No instante , o bloco passa pela posição , e no mesmo instante, um outro bloco, de massa m, é solto sobre o primeiro bloco e a nele se fixa. Qual é o gráfico que melhor representa a posição do primeiro bloco em função do tempo?

A figura mostra as curvas obtidas em três experimentos diferentes para o deslocamento horizontal em relação à posição de equilíbrio, , de um mesmo sistema bloco-mola que oscila descrevendo um movimento harmônico simples. Qual alternativa é correta?

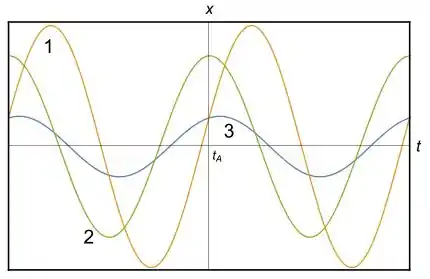
(a) Em , o módulo da aceleração do bloco no experimento 2 é menor que no experimento 1 e maior que no experimento 3.

(b) Em , a energia potencial elástica no experimento 1 é maior que a energia potencial elástica nos experimentos 2 e 3, sendo a energia potencial elástica no experimento 3 menor que no experimento 2.

(c) Em , o módulo da velocidade do bloco no experimento 1 é maior que nos experimentos 2 e 3.

(d) A freqüência angular do sistema nos três experimentos é diferente.

(e) Em , a energia cinética do bloco no experimento 2 é maior que no experimento 3.

O pêndulo A mostrado na figura consiste em uma esfera muito pequena de massa sustentado por uma corda de massa desprezível e comprimento . O pêndulo B consiste em uma esfera muito pequena de massa e uma barra delgada de massa e comprimento L. Sejam e os tempos que cada pêndulo demora em completar uma oscilação. Para deslocamentos pequenos em relação à posição de equilíbrio, pode-se dizer que:

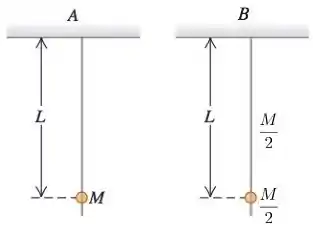
(a) Os dois pêndulos levam o mesmo tempo para completar uma oscilação, com .

(b) O pêndulo B demora menos tempo que o pêndulo A em completar uma oscilação, com .

(c) O pêndulo B demora menos tempo que o pêndulo A em completar uma oscilação, com

(d) O pêndulo B demora mais tempo que o pêndulo A em completar uma oscilação, com .

(e) O pêndulo B demora mais tempo que o pêndulo A em completar uma oscilação, com .

Formulário:

• Momentos de inércia de uma barra delgada de massa M e comprimento L em relação a um eixo que passa perpendicularmente:

– Pelo centro de massas da barra: .

– Por uma das extremidades da barra: .

• Teorema dos eixos paralelos: .

Um pêndulo formado por uma esfera de massa e raio desprezível está suspenso verticalmente a partir do ponto através de uma haste rígida de massa desprezível e comprimento . A haste está ligada a duas molas idênticas de constantes elásticas , massas desprezíveis, situadas a uma distância de como mostrado na figura (a). As molas estão relaxadas (isto é nem esticadas, nem comprimidas) quando o pêndulo está na posição vertical. Para iniciar o balanço do pêndulo, você o desloca com as mãos até que a haste forme um pequeno ângulo com a vertical, liberando-o a partir do repouso [figura (b)].

Dica: como o ângulo é pequeno, considere que as molas permanecem essencialmente na horizontal durante todo o movimento.

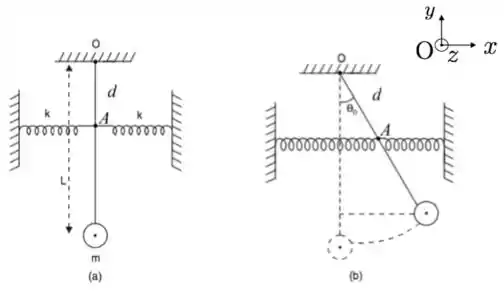
(a) Utilize o sistema de coordenadas da figura e obtenha a equação que descreve o movimento do pêndulo.

(b) Para pequenas oscilações em relação à posição de equilíbrio do pêndulo, determine a freqüência angular de oscilação.

(c) Obtenha a função para pequenas oscilações em relação à posição de equilíbrio.

SUGESTÕES:

• Item (a): Determine o(s) torque(s) em torno ao eixo de rotação ou utilize considerações energéticas.