P3 de Física 2 da USP - 2015

No oscilador harmônico amortecido pode-se dizer que a frequência de oscilação é, em relação à frequência do oscilador livre ,

(a) menor porque o módulo da aceleração média é reduzida pela força dissipativa.

(b) maior porque a amplitude do movimento é reduzida devido à dissipação de energia.

(c) igual porque os efeitos sobre a aceleração e sobre a amplitude se cancelam.

(d) maior porque a força dissipativa é oposta à velocidade.

(e) nenhuma das anteriores.

Um oscilador forçado sem amortecimento terá amplitude:

1. Dependente da frequência da força externa.
2. Que aumentará indefinidamente com o tempo.
3. Infinitamente grande já a partir do instante inicial, pois a energia não é dissipada.
4. Independente da frequência da força externa.
5. Nenhuma das Anteriores.

Um oscilador amortecido tem frequência igual a daquela que teria () se sua constante de amortecimento fosse nula. Ao aplicarmos uma força externa cossenoidal, a frequência de ressonância (máxima amplitude) é (Dado: , .).

1. 0, 8
3. 1, 6

Considere um oscilador amortecido e sujeito a uma força cossenoidal. As condições iniciais do oscilador podem

1. Ampliar ou reduzir a amplitude nos instantes iniciais do movimento.
2. Influenciam a amplitude do movimento mesmo em instantes muito posteriores ao início do movimento.
3. Não têm qualquer influência sobre o movimento.
4. Só podem aumentar a amplitude no início, pois o amortecimento reduzirá a amplitude de oscilação até o oscilador parar completamente.
5. Só podem aumentar a amplitude no início, pois o amortecimento reduzirá a amplitude de oscilação até um valor constante não nulo.

Um redutor de velocidades é feito com ondulações aproximadamente senoidais construídas na pista de uma rodovia. Deseja-se que a velocidade dos automóveis seja inferior a . Considere que a massa de um automóvel é de igualmente distribuída entre as rodas, e que os amortecedores independentes de cada roda têm uma mola de constante elástica mergulhada num fluido de viscosidade . O engenheiro decide que o redutor deve ser tal que o automóvel tenha a máxima amplitude de oscilação induzida pelas ondulações da pista exatamente quando o automóvel passa à velocidade pelo redutor.

Qual deve ser a distância entre as ondulações da pista?

Um oscilador harmônico com amortecimento está em repouso na posição de equilíbrio quando é submetido a uma aceleração senoidal = ). Equação de movimento do tipo .

a) Sendo , qual a frequência da aceleração para que a amplitude final de oscilação (regime estacionário, ) seja máxima?

b) Mantendo-se a frequência anterior e reduzindo-se o amortecimento para , qual o aumento relativo da amplitude de oscilação final?

c) Qual o período do batimento que surge no início do movimento se e ?

d) Encontre a função que descreve o movimento em função do tempo, , durante o regime transitório com .

Na figura abaixo, os períodos dos regimes transitório e estacionário são:

1. e
2. e
3. e
4. e
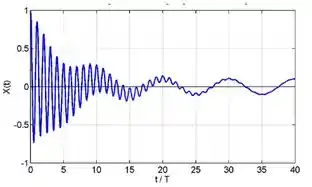
5. e

Dois sistemas massa mola encontram-se acoplados como mostra a figura. Sendo e a chamada razão áurea, o sistema tem dois modos normais com frequências e tais que:

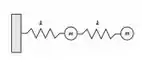
Observação: Existe um erro no enunciado: . O correto é . Além disso, não encontramos uma resposta que esteja listada acima.