Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Oscilador Linear Massa-Mola

Ver Teoria
Exercício 4612345678910111213141516171819202122232425262728293031323334353637383940414243444547484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

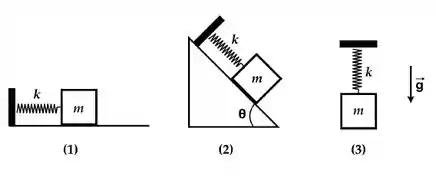
A figura mostra três osciladores harmônicos de mesma massa m e constante elástica k . Não há atrito entre o bloco e as superfícies de contato, nem resistência do ar. Pode-se dizer das frequências angulares naturais de oscilação ω o   que

  1. ω 0 1 = ω 0 2 = ω o 3
  2. ω 0 1 < ω 0 2 < ω o 3
  3. ω 0 3 < ω 0 2 < ω o 1
  4. ω 0 1 < ω 0 3 < ω o 2
  5. ω 0 2 < ω 0 1 < ω o 3

Passo 1

Os osciladores 2 e 3 diferem do oscilador 1 pela presença de forças resultantes f = m g s i n θ   e   f = - m g ao longo da vertical, respectivamente. Tais forças alteram a posição em torno da qual as oscilações harmônicas ocorrem, mas não a frequência natural da oscilação. Isto pode ser demonstrado diretamente da equação diferencial para a coordenada do oscilador na presença da força restauradora da mola e da força constante f :

m x ˙ ˙ = - k x + f = 0

x ˙ ˙ + ω o 2 x - f m = 0

Ou seja,

x ˙ ˙ + ω o 2 x x - f m ω o 2 = 0

Que em termos de uma nova variável z = x - f m ω o 2 é idêntica à do oscilador 1

z ˙ ˙ + ω o 2 z = 0

z = A c o s ω o t + ϕ

x t = f m ω o 2 + A c o s ω o t + ϕ

Ou seja, as oscilações ocorrem em torno da posição x e q = f m ω o 2 com frequência angular

ω o = k m , logo

ω 0 1 = ω 0 2 = ω o 3

Para o oscilador 2, a posição de equilíbrio estaria m g s i n θ k abaixo da posição relaxada da mola e para o oscilador 3, estaria m g k abaixo da posição relaxada da mola.

Resposta

Letra a

Exercícios de Livros Relacionados

Na figura, um bloco pesando 14,0N , que pode deslizar sem atrito em um plano inclinado de ângulo θ = 40,0 ° , está ligado ao alto do plano inclinado por uma mola de massa desprezível de 0,450m de comp
Um oscilador é formado por um bloco preso a uma mola ( k = 400N / m ). Em um certo instante t , a posição (medida a partir da posição de equilíbrio do sistema), a velocidade e a aceleração do bloco sã
Um bloco de 1,2k g deslizando em uma superfície horizontal sem atrito está preso a uma mola horizontal com k = 480N / m . Seja x o deslocamento do bloco a partir da posição na qual a mola se encontra
A figura mostra uma massa de 1,0k g colocada sobre uma massa de 5,0k g que oscila sobre uma superfície sem atrito. A constante elástica é de 50N / m , e o coeficiente de atrito estático entre os dois
A figura mostra um bastão homogêneo de 200g com um orifício em uma das extremidades. A outra extremidade é presa a uma mola horizontal. Quando o bastão está suspenso exatamente na vertical, a mola não