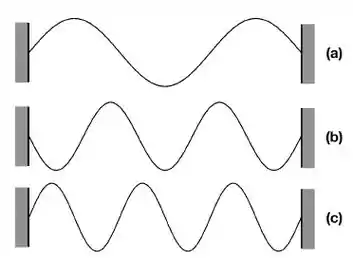
A figura mostra fotografias de diferentes modos de vibração de uma corda de de comprimento e densidade linear , presa por ambas as extremidades e submetida a uma tensão de . As frequências de oscilação transversal da corda para os três casos são
Passo 1
De cima para baixo, os modos apresentados na figura correspondem ao , respectivamente. As frequências dos modos normais de uma corda presa por ambas as extremidades são dadas por:
Onde
e é o comprimento da corda.
Logo
Portanto,
Resposta
Letra b
Exercícios de Livros Relacionados
Na figura, uma corda presa a um oscilador senoidal no ponto P e apoiada em um suport no ponto Q é tensionada por um bloco de massa m . A distância entre P e Q é L = 1,20 m e a freqüência do oscilador
Na figura, uma corda, presa a um oscilador senoidal no ponto P e apoiada em um suporte no ponto Q , é tensionada por um bloco de massa m . A distância entre P e Q é L=1,20m , a massa específica linear
A equação de uma onda transversal que se propaga em uma corda é y = 0,15 s e n ( 0,79 x - 13 t ) onde xey estão em metros e t está em segundos. (a) Qual é o deslocamento y em x=2,3m e t=0,16s ? Uma se
Utna corda d e120c m de comprimento está esticada entre dois suportes fixos. Qual é (a) o maior, (b) o segundo maior e (c) o terceiro mnaior comprimento de onda das ondas que se propagam na corda para
Uma onda estacionária em uma corda é descrita por y x , t = 0,40 s e n 5 π x cos 40 π t Onde xey estão em metros, e t em segundos. Para x ≥ 0 qual é a localização do nó com (a)o menor (b) o segundo