PSUB de Física 2 da USP - 2019

. A máxima potência dissipada é:

. A frequência de batimento entre o segundo harmônico de uma onda sonora em um tubo de órgão aberto em ambas as extremidades e o segundo harmônico de uma onda sonora em um tubo de órgão fechado em uma das extremidades é , sendo o som mais agudo no órgão fechado. Considerando que a velocidade do som no ar é , e que a frequência fundamental da onda sonora no órgão que tem uma das extremidades fechadas é , podemos afirmar que o comprimento do órgão aberto em ambas extremidades é:

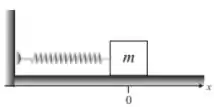
O gráfico mostra a posição em função do tempo de uma partícula de massa , ligada a uma mola de massa desprezível, que move-se em movimento retilíneo, sobre uma mesa horizontal lisa, na direção do eixo x, orientado para a direita.

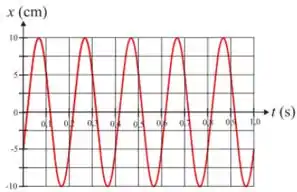
. Podemos afirmar que o instante exato que a partícula estará passando pelo ponto de equilíbrio e movendo-se para a direita, durante o primeiro período do movimento, é:

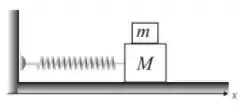
. Um bloco de massa está ligado a uma mola de constante elástica e apóia-se sobre um plano horizontal sem atrito. Um outro bloco, de massa , está no topo do bloco de massa . Se o coeficiente de atrito estático entre os dois corpos é , a distância máxima que os dois corpos podem ser puxados a partir da posição de equilíbrio sem que o bloco de cima escorregue, uma vez que os dois sejam librados é:

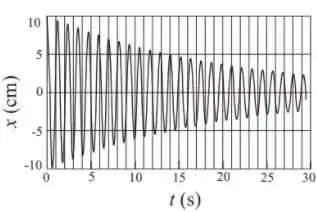
. O gráfico abaixo representa a posição em função do tempo de uma partícula de massa , que realiza um movimento harmônico amortecido, sujeita a uma força onde é a constante de amortecimento e é a velocidade do oscilador. Podemos afirmar que o valor da constante (definida como ) para este movimento é, aproximadamente:

O gráfico mostra a posição em função do tempo de uma partícula de massa , ligada a uma mola de massa desprezível, que move-se em movimento retilíneo, sobre uma mesa horizontal lisa, na direção do eixo x, orientado para a direita.

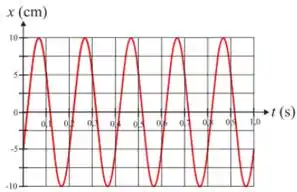
. Se o movimento realizado pela massa é um e a sua posição de equilíbrio ocorre em , podemos afirmar que a expressão da posição da partícula em função do tempo,

no sistema , é dada por:

. Uma corda, presa em suas extremidades, está vibrando como uma onda estacionária. A onda estacionária é produzida pela superposição de duas ondas senoidais, e , que têm a mesma frequência, a mesma velocidade, e as mesmas amplitudes, mas que propagam-se ao longo da corda em sentidos opostos. A vibração da corda, no , é representada pela equação:

onde é o deslocamento transversal de um elemento qualquer da corda na posição e no

instante . Para a onda estacionária descrita pela função , podemos afirmar que a função da

componente , que se desloca no sentido positivo do eixo é dada por:

. Considere as seguintes afirmações:

- A frequência de um oscilador amortecido é sempre menor que a sua frequência natural.

- O amortecimento crítico é a condição em que uma partícula retorna ao equilíbrio com a maior rapidez, quando comparado com o amortecimento supercrítico.

- Um oscilador forçado, com coeficiente de amortecimento igual a zero , oscila com

a frequência da força motriz externa.

- Se a constante de amortecimento é nula , o oscilador harmônico forçado tem amplitude máxima , quando a frequência angular da força motriz e a frequência natural do oscilador são iguais, sendo o máximo valor da força motriz e a massa do oscilador.

- A solução geral do problema de um oscilador harmônico forçado é uma oscilação com a

frequência da força motriz externa.

- A altura da curva de ressonância da amplitude em função da frequência de um oscilador

harmônico amortecido e forçado aumenta com o aumento da constante de amortecimento .

- A largura da curva de ressonância da amplitude em função da frequência de um oscila-

dor harmônico amortecido e forçado aumenta com o aumento do coeficiente de amortecimento .

O número de afirmações corretas é:

. Uma partícula de massa , presa a uma mola de constante elástica , inicialmente em repouso na condição de equilíbrio em , recebe um impulso que lhe confere uma velocidade de , entrando em oscilação. Se a partícula movimenta-se sobre uma mesa lisa, mas está sujeita a uma força amortecedora do tipo com , a função que descreve o deslocamento da partícula em função do tempo , no sistema , em relação à origem é: