P1 de Física 3 - FIS1051 da PUCRIO - 2012.2

Uma esfera metálica maciça de raio é concentricamente circundada por uma casca esférica metálica com raios interno e externo , como mostrado na figura abaixo.

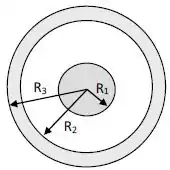
O fluxo elétrico através de uma superfície esférica gaussiana de raio vale . Sabendo que a esfera maciça possui uma carga e considerando que e :

Calcule, utilizando a Lei de Gauss, a distribuição das cargas nas superfícies externa e interna da casca esférica. Qual é o valor da carga líquida da casca? Justifique as afirmações e os cálculos.

Calcule o valor do módulo do campo elétrico na superfície da esfera maciça e na superfície externa da casca.

Considere agora que a casca esférica metálica é substituída por uma casca esférica isolante com e (desenho abaixo). A casca isolante é carregada uniformemente com uma carga igual ao valor da carga líquida da casca metálica anterior.

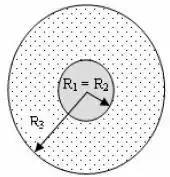
Calcule o valor do fluxo elétrico através de uma superfície gaussiana esférica de raio .

Uma distribuição continua de cargas é constituída por um anel de raio , com densidade linear de carga uniforme , e um anel fracionado concêntrico de raio e densidade linear de carga uniforme , ambos no plano e com o mesmo eixo .

O anel fracionado é constituído por quatro arcos de circunferências idênticos, e cada arco é separado do seguinte por um ângulo , conforme a figura abaixo.

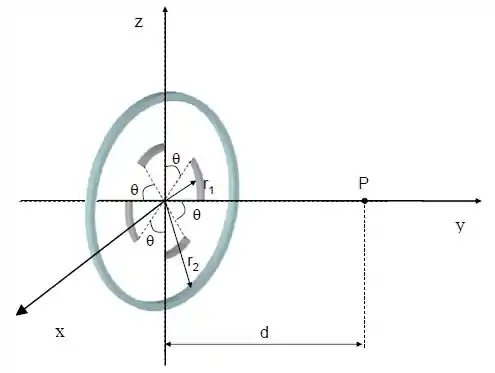
Calcule o potencial elétrico gerado pela distribuição de carga no ponto que se encontra sobre o eixo a uma distancia da origem.

Se o anel fracionado for girado de um ângulo arbitrário entorno do seu eixo, o resultado mudaria? Justifique as suas afirmações.

Qual deve ser o valor da razão para o potencial no ponto ser igual a zero?

Trace o gráfico de em função do ângulo . Descreva o andamento encontrado justificando as suas afirmações.

Uma barra isolante, de espessura desprezível e comprimento , repousa sobre o eixo desde até . Ela recebe uma carga total que se distribui de modo não uniforme de acordo com a densidade linear de carga dada pela função , onde é uma constante com dimensões apropriadas. O sistema de coordenadas está indicado na figura.

Calcule o valor da carga total na barra, , e a unidade SI (Sistema Internacional) da constante .

Calcule o valor (componente apenas) do vetor campo elétrico no ponto de coordenadas .

O campo elétrico produzido por toda a barra no ponto , de coordenadas , vale . Em que ponto do espaço se deveria colocar a carga pontual para que o campo total resultante fosse nulo em ?