Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Corpos Extensos

Ver Teoria
Exercício 181234567891011121314151617192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Densidade de Carga, Potencial Elétrico

Uma distribuição continua de cargas é constituída por um anel de raio r 2 = 10   a , com densidade linear de carga uniforme λ 2 > 0 , e um anel fracionado concêntrico de raio r 1 = a e densidade linear de carga uniforme λ 1 > 0 , ambos no plano X Z e com o mesmo eixo Y .

O anel fracionado é constituído por quatro arcos de circunferências idênticos, e cada arco é separado do seguinte por um ângulo θ , conforme a figura abaixo.

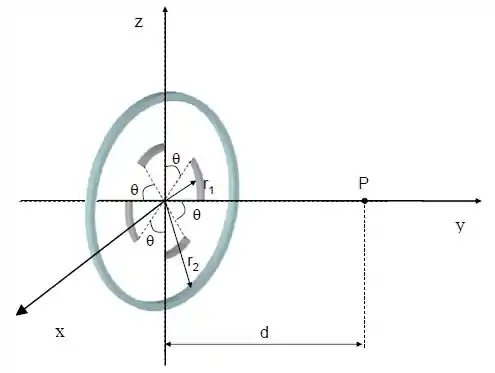
a ) Calcule o potencial elétrico gerado pela distribuição de carga no ponto P que se encontra sobre o eixo y a uma distancia d = 15   a da origem.

b ) Se o anel fracionado for girado de um ângulo β arbitrário entorno do seu eixo, o resultado mudaria? Justifique as suas afirmações.

c ) Qual deve ser o valor da razão λ 2 / λ 1 para o potencial no ponto P ser igual a zero?

d ) Trace o gráfico de λ 2 / λ 1 em função do ângulo θ . Descreva o andamento encontrado justificando as suas afirmações.

Passo 1

a ) Calcule o potencial elétrico gerado pela distribuição de carga no ponto P que se encontra sobre o eixo y a uma distancia d = 15   a da origem.

Pra não começarmos nos complicando muito, vamos calcular o potencial de cada distribuição separado, de forma que:

V = V 1 + V 2

Beleza?

  • V 2

    • Vamos começar com esse cara que parece ser mais comum.

    O segredo aqui é começar escrevendo o potencial d V 2 gerado por uma carga infinitesimal d q , de forma que:

    d q = λ 2   d l

    Como o elemento d l corresponde a um pedaço infinitesimal da circunferência, podemos dizer que d l = r 2 d θ ' .

    Logo:

    d q = r 2 λ 2   d θ '

    Obs.: Chamei esse cara aqui de d θ ' pra diferenciar do θ do desenho, beleza?!

    Portanto, o potencial d V 2 pode ser escrito como:

    d V 2 = 1 4 π ϵ 0 d q r

    d V 2 = r 2 λ 2 4 π ϵ 0 d θ ' r

    Onde r é a distância entre um ponto da circunferência de raio r 2 ao ponto P . Portanto:

    r = d 2 + r 2 2

    d V 2 = r 2 λ 2 4 π ϵ 0 d θ ' d 2 + r 2 2

    Por último, só temos que integrar esse cara. Como aqui se trata de uma circunferência completa, 0 ≤ θ ≤ 2 π .

    V 2 = 1 4 π ϵ 0 r 2 λ 2 d 2 + r 2 2 ∫ 0 2 π d θ '

    V 2 = 1 4 π ϵ 0 2 π r 2 λ 2 d 2 + r 2 2

    Pra fechar, só temos que substituir r 2 = 10   a e d = 15   a :

    V 2 = 1 4 π ϵ 0 2 π 10 a λ 2 15 a 2 + 10 a 2

    Simplificando esse cara:

    V 2 = 1 4 π ϵ 0 2 π 10 a λ 2 2 5 a 2

    V 2 = 1 4 π ϵ 0 2 π 10 a λ 2 5 a

    Finalmente:

    V 2 = 1 4 π ϵ 0 2 π 10 λ 2 5

    Passo 2

  • V 1

Agora que entendemos como calcular o potencial para o caso de uma circunferência, vamos usar a mesma ideia aqui para esses arcos de raio r 1 .

Lembrando que o problema disse que o anel fracionado é constituído por quatro arcos de circunferências idênticos.

Logo:

V 1 = 4 V 1 '

Onde V 1 ' corresponde ao potencial de cada arco.

Como eu tinha falado a ideia aqui é a mesma de antes... isso significa que podemos escrever agora o potencial d V 1 ' gerado por uma carga infinitesimal por:

d V 1 ' = r 1 λ 1 4 π ϵ 0 d θ ' d 2 + r 1 2

Obs.: Chamei esse cara aqui de d θ ' pra diferenciar do θ do desenho, beleza?!

A pergunta agora é: quais serão os limites de integração para θ ' ?

Lembra que o problema disse que cada arco está separado do outro por um ângulo θ ? Isso significa que θ ' vai variar de 0 até π 2 - θ . Olha pra figura e tenta enxergar... conseguiu?

Logo:

V 1 ' = 1 4 π ϵ 0 r 1 λ 1 d 2 + r 1 2 ∫ 0 π 2 - θ d θ '

V 1 ' = 1 4 π ϵ 0 r 1 λ 1 d 2 + r 1 2 π 2 - θ

Novamente, pra finalizar, temos apenas que substituir os valores r 1 = a e d = 15   a .

V 1 ' = 1 4 π ϵ 0 a λ 1 15 a 2 + a 2 π 2 - θ

Agora é só darmos um jeito nessa bagunça:

V 1 ' = 1 4 π ϵ 0 a λ 1 16 a 2 π 2 - θ

V 1 ' = 1 4 π ϵ 0 a λ 1 4 a π 2 - θ

V 1 ' = 1 4 π ϵ 0 a λ 1 4 a π 2 - θ

V 1 ' = 1 4 π ϵ 0 λ 1 4 π 2 - θ

Logo:

V 1 = 4 V 1 '

V 1 = 4   1 4 π ϵ 0 λ 1 4 π 2 - θ

V 1 = 1 4 π ϵ 0 λ 1 π 2 - θ

Finalmente:

V = V 1 + V 2

V = 1 4 π ϵ 0 λ 1 π 2 - θ + 2 π 10 λ 2 5

Passo 2

b ) Se o anel fracionado for girado de um ângulo β arbitrário entorno do seu eixo, o resultado mudaria? Justifique as suas afirmações.

O potencial depende somente da distância entre os elementos de carga do anel fracionado para o ponto P . Como vimos anteriormente, por causa da geometria do problema, essas distâncias são constantes.

Assim, se girarmos o anel fracionado de um ângulo β em torno do seu eixo, as distâncias dos elementos de carga para o ponto P permanecerão as mesmas. Sendo assim, o resultado não mudaria.

Passo 3

c ) Qual deve ser o valor da razão λ 2 / λ 1 para o potencial no ponto P ser igual a zero?

Opa! Agora até que está tranquilo pro nosso lado...

Vimos na letra a que o potencial no ponto P é dado por:

V = 1 4 π ϵ 0 λ 1 π 2 - θ + 2 π 10 λ 2 5

Então, a única coisa que temos que fazer aqui é igualar V a zero.

V = 1 4 π ϵ 0 λ 1 π 2 - θ + 2 π 10 λ 2 5 = 0

Agora é só organizar esse cara até encontrarmos a expressão para λ 2 / λ 1 :

λ 1 π 2 - θ + 2 π 10 λ 2 5 = 0

2 π 10 λ 2 5 = - λ 1 π 2 - θ

2 π 10 λ 2 5 = λ 1 θ - π 2

λ 2 λ 1 = 5 2 π 10 θ - π 2  

Racionalizando esse cara:

λ 2 λ 1 = 5 10 2 π 10 θ - π 2

λ 2 λ 1 = 10 4 π θ - π 2

Opa! Encontramos um resultado bonitinho, certo?!

Nãaaaaaaaaaao!

Temos um problema sério aqui. Acontece que θ necessariamente é menor que π / 2 , isso significa que o resultado disso é um valor negativo para a razão λ 2 / λ 1 .

Ok... mas onde está o problema?

O problema é que o enunciado nos disse que λ 2 e λ 1 são positivos. Sendo assim, a razão λ 2 / λ 1 jamais daria um valor negativo.

Portanto, não existe valor para a razão λ 2 / λ 1 de forma que o potencial no ponto P seja nulo.

Passo 4

d ) Trace o gráfico de λ 2 / λ 1 em função do ângulo θ . Descreva o andamento encontrado justificando as suas afirmações.

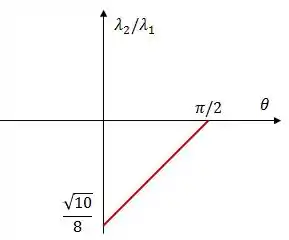
Resposta

a )

V = 1 4 π ϵ 0 λ 1 π 2 - θ + 2 π 10 λ 2 5

b )

O resultado não mudaria.

c )

Não existe valor para a razão λ 2 / λ 1 de forma que o potencial no ponto P seja nulo.

d )

Exercícios de Livros Relacionados

Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força