Campo Elétrico, Densidade de Carga, Campos Elétricos e Corpos Carregados
Uma barra isolante, de espessura desprezível e comprimento , repousa sobre o eixo desde até . Ela recebe uma carga total que se distribui de modo não uniforme de acordo com a densidade linear de carga dada pela função , onde é uma constante com dimensões apropriadas. O sistema de coordenadas está indicado na figura.
Calcule o valor da carga total na barra, , e a unidade SI (Sistema Internacional) da constante .
Calcule o valor (componente apenas) do vetor campo elétrico no ponto de coordenadas .
O campo elétrico produzido por toda a barra no ponto , de coordenadas , vale . Em que ponto do espaço se deveria colocar a carga pontual para que o campo total resultante fosse nulo em ?
Passo 1
Calcule o valor da carga total na barra, , e a unidade SI (Sistema Internacional) da constante .
Por definição, a densidade linear de carga é dada por:
Nesse caso, como a barra está posicionada ao longo do eixo :
Onde e .
Passo 2
Pra encontrar a unidade SI da constante , basta analisarmos as unidades dos termos da equação de densidade linear de carga:
Portanto, a unidade da constante é .
Passo 3
Calcule o valor (componente apenas) do vetor campo elétrico no ponto de coordenadas .
Pra começar, vamos começar calculando o campo elétrico gerado por uma carga infinitesimal :
Graficamente, a ideia é essa:
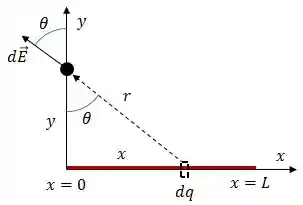
Onde:
Logo:
Como estamos interessados somente na componente vertical, na direção :
Reorganizando esse cada:
Passo 4
Finalmente, só temos que integrar esse cara entre e :
Essa não é uma integral difícil de resolver, ela pode ser resolvida através de uma substituição. Entretanto, o seu formulário contém as respostas de algumas integrais, e como esse tipo de integral costuma aparecer bastante nesse tipo de problema, é bem provável que a resposta dessa integral esteja no seu formulário... é só dar uma olhada.
Pra finalizar, temos apenas que substituir os valores aqui:
Substituindo os valores:
Agora só temos que organizar essa bagunça até chegar no resultado final:
Passo 5
O campo elétrico produzido por toda a barra no ponto , de coordenadas , vale . Em que ponto do espaço se deveria colocar a carga pontual para que o campo total resultante fosse nulo em ?
Logo de cara, o módulo do campo elétrico gerado pela caga no ponto deve ser igual ao módulo do campo elétrico gerado pela barra no ponto , para que elas possam se anular. Isso já vai nos ajudar a descobrir a distâncias entre e .
Substituindo os valores, onde , teremos:
Beleza, agora que já sabemos que a carga deve estar a do ponto , temos que dizer se ele está à direita ou à esquerda do ponto .
Bom, o campo elétrico gerado pela barra, no ponto , possui o seguinte sentido:
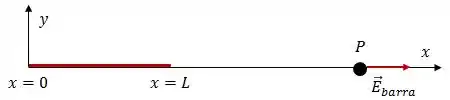
Como é uma carga negativa, o campo gerado por ela aponta para a própria carga. Assim, para que o campo gerado pela carga esteja no sentido oposto ao campo gerado pela barra, a carga deve estar à esquerda do ponto .
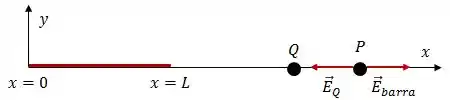
Logo, o ponto em que a carga deve estar para que o campo elétrico no ponto seja nulo é:
O ponto é .
Resposta