P2 de Física 3 - FIS1051 da PUCRIO - 2020.2

Na figura abaixo um fio retilíneo muito longo conduz uma corrente e uma espira

retangular de lados conduz uma corrente . Suponha que e e .

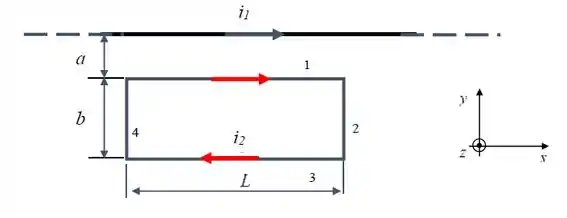
Calcule a força magnética F total (módulo, direção e sentido) a que está submetida espira.

Um fio retilíneo muito longo, alinhado com o eixo x e transportando uma corrente, é colocado num campo magnético externo uniforme de módulo , como representado na figura abaixo

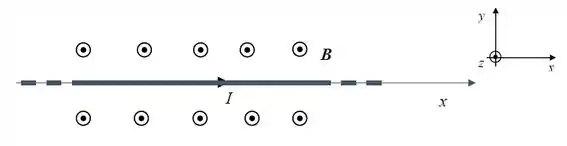Utilizando o sistema de referência indicado, determine os pontos no espaço onde o

campo magnético resultante é nulo.

Em uma região do espaço existe um campo magnético na direção cuja magnitude é função da posição no como:

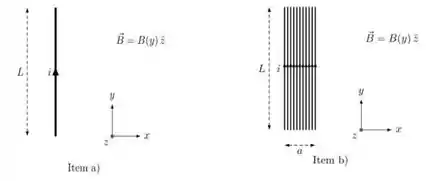a) Nessa região do espaço, colocamos um segmento linear de comprimento L percorrido por

uma corrente i. O segmento está orientado como mostra a figura, paralelo ao eixo-y com seu ponto inferior em y=0. Calcule o vetor força magnética total sentido pelo segmento.

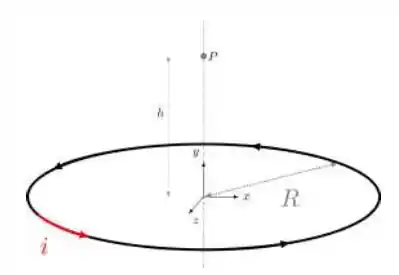
b) Considere um sistema composto de vários segmentos (ao invés de apenas um) de mesmo tamanho L muito finos e colocados um do lado do outro formando uma parede de segmentos com largura a como mostra a figura. A corrente total que atravessa esse sistema é i e agora está distribuída igualmente entre os segmentos. Qual é o valor do vetor força magnética sentido pelo sistema?

Considere uma espira circular de raio R no plano-xz com centro na origem do sistema de coordenadas, como mostra a figura. Essa espira é percorrida por uma corrente constante i no sentido anti-horário (também mostrado na figura).

a) Utilizando a Lei de Biot-Savart, encontre o valor do campo magnético total no ponto

mostrado na figura (o ponto se encontra no eixo-y).

b) Se introduzirmos nessa região do espaço um campo magnético externo constante:

calcule os vetores força magnética total e o torque na espira.

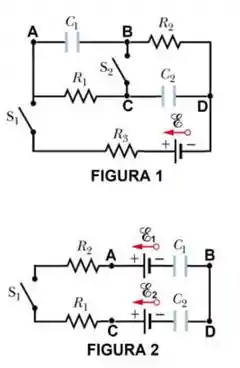
Considere o circuito da Figura 1, onde os valores de , são constantes e conhecidos. Inicialmente, os capacitores e estão descarregados e as chaves e abertas. Os capacitores e são carregados fechando-se as duas chaves simultaneamente. Em função dos dados do problema:

a) Apresente expressões para as tensões V1 e V2 e para as energias e armazenadas nos respectivos capacitores, supondo que ambas as chaves permaneceram fechadas durante muito tempo. Considere agora o circuito da Figura 2, onde os valores de , e são constantes e conhecidos. Inicialmente, os capacitores e estão descarregados e a chave S1 aberta. No instante , a chave é fechada e assim permanece por muito tempo. Em função dos dados deste novo problema:

b) Apresente expressões para as cargas nos capacitores e em função do tempo.

c) Apresente uma expressão para a tensão no resistor R1 em função do tempo.

d) Apresente expressões para as tensões e em função do tempo.