PUCRIO – Física 3 2020.2 – P2 – Questão 2B
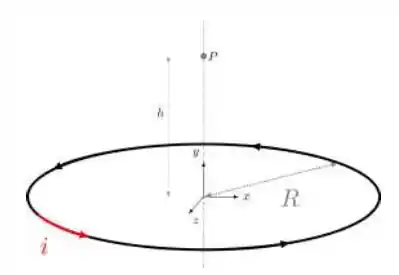
Considere uma espira circular de raio R no plano-xz com centro na origem do sistema de coordenadas, como mostra a figura. Essa espira é percorrida por uma corrente constante i no sentido anti-horário (também mostrado na figura).
a) Utilizando a Lei de Biot-Savart, encontre o valor do campo magnético total no ponto
mostrado na figura (o ponto se encontra no eixo-y).
b) Se introduzirmos nessa região do espaço um campo magnético externo constante:
calcule os vetores força magnética total e o torque na espira.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Letra (a):
Por simetria, temos que o campo resultante no ponto vai estar na direção . Assim:
E olhando a figura temos que é:
E pela lei de Biot-Savart o diferencial de campo é:
Beleza até aqui?
Passo 2
Letra (b):
A força resultante sobre uma espira fechada é zero! Então só precisamos calcular o torque! Sim, embora a força seja nula, o torque não é!
O torque é:
O momento é:
E o torque é:
Espero ter ajudado!