PUCRIO – Física 3 2020.2 – P2 – Questão 3C
Na figura abaixo um fio retilíneo muito longo conduz uma corrente e uma espira
retangular de lados conduz uma corrente . Suponha que e e .
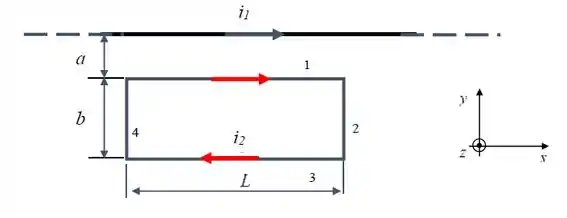
Calcule a força magnética F total (módulo, direção e sentido) a que está submetida espira.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
A primeira coisa ser notada que os lados e não contribuem para a força resultante! Então precisamos analisar as forças nos lados e .
Beleza até aqui?
Passo 2
Vou começar calculando a força no lado . A expressão para a força é:
O campo é devido à corrente , e esse lado está a uma distância do fio:
E o vetor deslocamento é no sentido da corrente :
Daí essa força é:
E o produto vetorial é:
Passo 3
Agora a força no lado . A diferença aqui é que a corrente está no sentido , e a distância desse lado até o fio é . Assim temos:
O campo é devido à corrente , e esse lado está a uma distância do fio:
E o vetor deslocamento é no sentido da corrente :
Daí essa força é:
E o produto vetorial é:
Passo 4
Podemos calcular, portanto a força resultante:
Espero ter ajudado!