PUCRIO – Física 3 2020.2 – P2 – Questão 3B
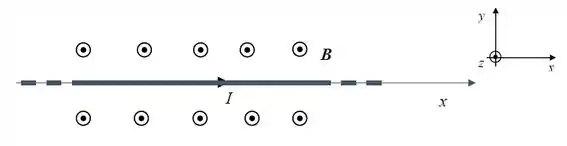
Um fio retilíneo muito longo, alinhado com o eixo x e transportando uma corrente, é colocado num campo magnético externo uniforme de módulo , como representado na figura abaixo
Utilizando o sistema de referência indicado, determine os pontos no espaço onde o
campo magnético resultante é nulo.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Letra (a):
Aqui temos que a soma dos campos (do fio e externo) deve ser zero:
Na região acima do fio o campo produzido por ele tem direção oposta ao campo externo, então é ali que teremos campo resultante nulo.
Beleza até aqui?
Passo 2
Vou começar calculando o campo do fio.
Usando a lei de ampére a uma distância do fio temos:
E para saber onde temos campo zero:
Agora é só isolar e substituir:
Espero ter ajudado!