P3 de Física 3 - FIS1051 da PUCRIO - 2020.2

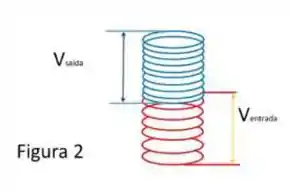
Um exemplo simplificado de um transformador de tensões pode ser visto na figura 2. Um sinal é aplicado aos terminais de um fio condutor perfeito (vermelho) que está enrolado NE vezes formando um solenóide (vermelho). Em frente a esse solenóide vermelho está um solenóide (azul) formado por um fio condutor perfeito de mesma área, com voltas. Um sinal de saída é, então, obtido nos terminais do solenóide azul.

NOTE: uma boa aproximação é considerar que todas as linhas de campo magnético geradas pelo solenóide de entrada (vermelho) atravessam também o solenóide azul de saída.

d)Desenhe duas linhas de campo magnético dentro dos solenóides.

e)Sendo o valor do fluxo magnético total gerado pelo sinal de entrada no solenóide vermelho, onde é o fluxo sobre uma única espira do solenóide vermelho. Obtenha então o fluxo magnético total sobre o solenóide de saída (azul).

f)Conclua o estudo obtendo a razão .

Um arame metálico, de resistência desprezível, forma um circuito circular, de raio , contendo um capacitor de capacitância , em série com um resistor de resistência igual a, como mostrado na figura 1. Este arame se encontra no plano x-y. A este sistema é aplicado um campo magnético, uniforme no espaço, dado por , onde e .

a) Calcule a instantânea sobre o aro como função do tempo.

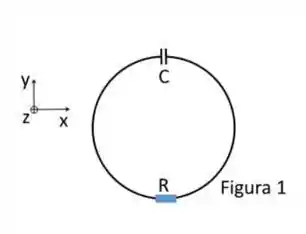b) Supondo que, em t = 0 s, o capacitor estava descarregado e a corrente no aro era nula, obtenha a carga instantânea sobre o capacitor e a corrente sobre o aro como função do tempo.

c) Calcule a potência total dissipada no resistor quando .

No circuito da figura abaixo, o gerador de corrente alternada tem o valor da tensão quadrática média igual a quando opera na frequência.

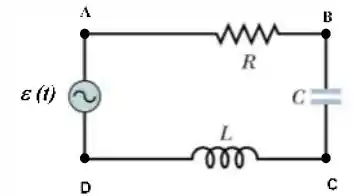
Sabendo que a indutância , a capacitância e que a resistência :

a) calcule os valores da tensão quadrática média entre os pontos: AB, BC e CD.

b) calcule os valores da tensão quadrática média entre os pontos: AC e BD.

c) Desenhe o diagrama de fasores do circuito indicando CLARAMENTE o valor de cada um deles. (Nota: cuidado para respeitar aproximadamente a escala entre os fasores).

d) Qual é o valor do ângulo de fase entre a corrente no circuito e a tensão do gerador?

e) Calcule o valor médio da potência fornecida pelo gerador.

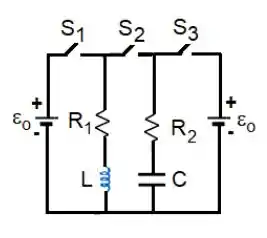
No circuito da Figura, o elemento conhecido tem o valor . Inicialmente, todas as chaves estão abertas, o capacitor está descarregado e não existe corrente no indutor.

Na FASE 1, as chaves e são fechadas simultaneamente (a chave permanece aberta). Imediatamente após o fechamento das chaves, medem-se as correntes no indutor e no resistor , sendo o tempo expresso em segundos. Com base nestas informações:

a) Determine os valores de R1 e L, indicando o sentido da corrente no indutor (para cima ou

para baixo) muito tempo após o fechamento da chave .

b) Calcule a energia armazenada no indutor muito tempo após o fechamento da chave .

c) Determine os valores de e .

d) Determine o valor do módulo das cargas no capacitor muito tempo após o fechamento da

chave , indicando se a carga positiva está na sua placa superior ou inferior.

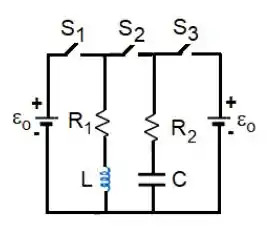
Muito tempo após o fechamento das chaves e , elas são abertas e a chave é fechada, dando início à FASE 2. Esta comutação é realizada de forma simultânea, não havendo perdas nas energias armazenadas no indutor e no capacitor. Com base nestas informações:

e) Determine de forma literal expressões para a carga no capacitor e a corrente no circuito relevante em função do tempo (medido em segundos a partir do início da FASE 2), de e, assim como da corrente inicial e da carga inicial no capacitor.

f) Determine de forma numérica expressões para a carga no capacitore a corrente no circuito relevante em função do tempo (medido em segundos a partir do início da FASE 2), usando os valores de e, assim como da corrente inicial e da carga inicial no capacitor, obtidos nos itens anteriores.