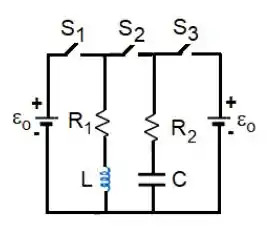
No circuito da Figura, o elemento conhecido tem o valor . Inicialmente, todas as chaves estão abertas, o capacitor está descarregado e não existe corrente no indutor.
Na FASE 1, as chaves e são fechadas simultaneamente (a chave permanece aberta). Imediatamente após o fechamento das chaves, medem-se as correntes no indutor e no resistor , sendo o tempo expresso em segundos. Com base nestas informações:
a) Determine os valores de R1 e L, indicando o sentido da corrente no indutor (para cima ou
para baixo) muito tempo após o fechamento da chave .
b) Calcule a energia armazenada no indutor muito tempo após o fechamento da chave .
c) Determine os valores de e .
d) Determine o valor do módulo das cargas no capacitor muito tempo após o fechamento da
chave , indicando se a carga positiva está na sua placa superior ou inferior.
Passo 1
Letra (a):
A equação de corrente quando há o carregamento do indutor é:
No enunciado foi nos dado essa equação, saca só:
Fazendo a comparação temos o seguinte:
A força eletromotriz inicial é , então daqui já conseguimos encontrar o valor de :
Certo? Só falta determinar o valor da indutância. Dá uma olhada no argumento da exponencial. Conseguimos comparar esses dois valores também:
Já sabemos o valor da resistência, então podemos encontrar o valor de :
E o sentido é para baixo.
Beleza até aqui?
Passo 2
Letra (b):
Para o indutor se comporta como um fio condutor normal, sendo assim, a corrente que passa por ele pode-se ser descoberta pela lei de ampére aplicada no resistor:
Ou também pode ser encontrada a partir equação para a corrente no indutor e fazendo .
E daí a energia armazenada é:
Passo 3
Letra (c):
Agora o problema pede os valores de e . Da equação para a corrente no capacitor temos:
E comparando com a equação que foi fornecida temos:
A fornecida é , então podemos encontrar a resistência:
E comparando os argumentos das exponenciais, podemos encontrar a capacitância:
Daí temos:
Passo 4
Letra (d):
Para , a tensão no capacitor é a do sistema, daí a carga é máxima:
Espero ter ajudado!