PUCRIO – Física 3 2020.2 – P3 – Questão 1
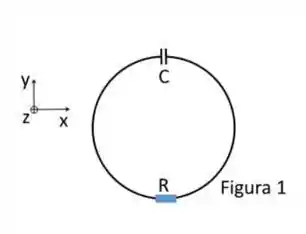
Um arame metálico, de resistência desprezível, forma um circuito circular, de raio , contendo um capacitor de capacitância , em série com um resistor de resistência igual a, como mostrado na figura 1. Este arame se encontra no plano x-y. A este sistema é aplicado um campo magnético, uniforme no espaço, dado por , onde e .
a) Calcule a instantânea sobre o aro como função do tempo.
b) Supondo que, em t = 0 s, o capacitor estava descarregado e a corrente no aro era nula, obtenha a carga instantânea sobre o capacitor e a corrente sobre o aro como função do tempo.
c) Calcule a potência total dissipada no resistor quando .
Passo 1
Fala galera, tudo bem?
Letra (a):
A surge da variação do fluxo sobre a espira, certo? O fluxo magnético é:
Como o campo é na direção de e o vetor normal à área da espira, então o ângulo entre eles é e . A única quantidade que varia com o tempo é o campo, então derivando em relação ao tempo o fluxo, temos a fem induzida:
Os dados são:
Agora é só substituir:
Tranquilo?
Passo 2
Quando olhamos para a espira como um circuito, temos um circuito . A equação diferencial que descreve esse circuito é:
E a solução da carga (carregamento do capacitor) em função do tempo para essa equação é:
Os dados são:
Agora é só substituir:
E a carga em função do tempo é:
E agora a corrente. Na situação de carregamento, a expressão para corrente num circuito é:
Beleza até aqui?
Passo 3
Letra (c):
E a potência dissipada pelo resistor é:
Espero ter ajudado!