Muito tempo após o fechamento das chaves e , elas são abertas e a chave é fechada, dando início à FASE 2. Esta comutação é realizada de forma simultânea, não havendo perdas nas energias armazenadas no indutor e no capacitor. Com base nestas informações:
e) Determine de forma literal expressões para a carga no capacitor e a corrente no circuito relevante em função do tempo (medido em segundos a partir do início da FASE 2), de e, assim como da corrente inicial e da carga inicial no capacitor.
f) Determine de forma numérica expressões para a carga no capacitore a corrente no circuito relevante em função do tempo (medido em segundos a partir do início da FASE 2), usando os valores de e, assim como da corrente inicial e da carga inicial no capacitor, obtidos nos itens anteriores.
Passo 1
Letra (e):
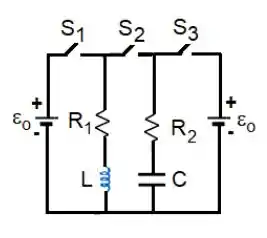
Muito tempo depois das chaves e serem abertas, elas são fechadas significa que tanto o capacitor, quanto o indutor estão carregados. Quando fechamos apenas a chave , temos um circuito série com resistência equivalente igual a , pois temos dois resistores em série. As fontes ficam de fora dessa vez.
A equação diferencial que descreve esse circuito é:
Dividindo tudo por e multiplicando por (-1) temos:
Aqui temos uma equação diferencial de segunda ordem homogênea. Vou reescrever a constante , assim temos:
Passo 2
A técnica para resolver essa equação é achar a equação característica, em termos de . Se você não lembra, dá uma olhadinha nessa parte no nosso site que ta super maneiro!
A equação característica da nossa equação diferencial é:
E a solução para ela é:
A solução dessa equação vai depender do sinal dessa raiz. Então precisamos determinar se esse circuito vai estar no regime crítico, supercrítico ou subcrítico.
Então vou resgatar os valores de e :
Então o valor de é:
Então temos que o regime desse circuito é subcrítico, quando temos raízes imaginárias. Daí a solução é:
Onde temos que .
A solução para essa equação diferencial associada é:
A resistência equivalente é , então a solução em termos dos parâmetros dados é:
Passo 3
A condição inicial nos diz que a carga em é máxima:
Sendo assim, , para termos carga máxima, daí a constante é:
Aí a solução final para a carga em função do tempo é:
Por fim, podemos derivar essa expressão em função do tempo e determinar a corrente nesse circuito:
Passo 4
Letra (f):
Os valores dos componentes são:
E podemos calcular :
Aí as expressões numéricas para a carga e a corrente em função do tempo são:
E a corrente:
Espero ter ajudado!