PUCRIO – Física 3 2020.2 – P3 – Questão 3
No circuito da figura abaixo, o gerador de corrente alternada tem o valor da tensão quadrática média igual a quando opera na frequência.
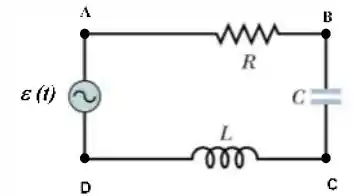
Sabendo que a indutância , a capacitância e que a resistência :
a) calcule os valores da tensão quadrática média entre os pontos: AB, BC e CD.
b) calcule os valores da tensão quadrática média entre os pontos: AC e BD.
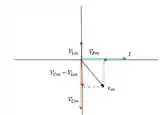
c) Desenhe o diagrama de fasores do circuito indicando CLARAMENTE o valor de cada um deles. (Nota: cuidado para respeitar aproximadamente a escala entre os fasores).
d) Qual é o valor do ângulo de fase entre a corrente no circuito e a tensão do gerador?
e) Calcule o valor médio da potência fornecida pelo gerador.
Passo 1
Letra (a):
Precisamos lembrar de algumas fórmulas para resolver essa questão:
Foi dada a freqüência , daí temos que .
Vou começar calculando as reatâncias:
A o valor de :
A corrente vai ser dada por:
Passo 2
Agora as :
Passo 3
Letra (b):
Seguindo o circuito e com os valores das ddps do passo anterior, podemos achar o que se pede.
- :
- :
Passo 4
Letra (c) e (d):
E agora o ângulo da corrente com a tensão:
Como o circuito é capacitivo.
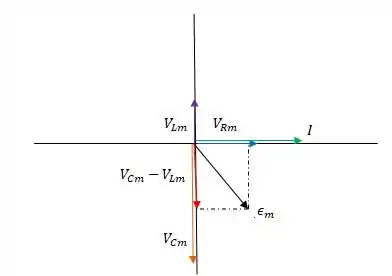
Como o vetor (em vermelho) aponta na vertical para baixo. Os fasores e (azul e verde respectivamente) apontam na horizontal para a direita. O fasor (em preto) fica no quarto quadrante, e faz um ângulo de no sentido negativo de rotação.
O diagrama dos fasores fica:
Passo 5
Letra (e):
A potência fornecida pelo gerador é:
O exercício não pede, mas vou calcular a potência dissipada pelo resistor. Sabemos que a potência fornecida pelo gerador é a mesma potência dissipada pelo resistor. Então vou fazer a prova real:
Olha que legal! Você sempre pode testar se seu resultado está correto fazendo isso, beleza?
Espero ter ajudado!
Resposta
