PF de Física 3 da UFRJ - 2014.2
Física 3 - UFRJ
Sabe-se que, no interior de um cilindro (circular reto) de raio , existe um campo magnético , onde são as coordenadas cilíndricas usuais, é uma constante, e o eixo coincide com o eixo de simetria do cilindro.
A energia magnética armazenada no cilindro entre e é
Ver solução completa
Considere dois pequenos dipolos elétricos: o primeiro encontra-se no eixo , com seu centro na origem , e é formado por partículas de cargas e , enquanto o segundo encontra-se no eixo e é formado por partículas de cargas e (conforme a figura).
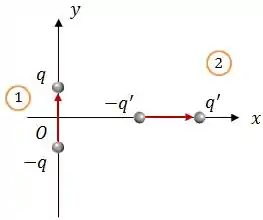
Seja a forca eletrostática exercida pelo dipolo 1 sobre o dipolo 2. Podemos afirmar que:
é nula e o torque sobre o dipolo 1 tende a girá-lo no sentido horário.
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido horário.
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido horário.
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido anti-horário.
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido anti-horário.
Ver solução completaUm capacitor possui placas paralelas separadas por uma distância igual a . O espaço entre as placas está cheio de poliéster (Constante dielétrica, ), que possui rigidez dielétrica . Qual a voltagem máxima, e a carga máxima possível que o capacitor pode suportar sem que ocorra ruptura dielétrica.
Considere que na ausência do poliéster o capacitor possui capacitância .
;
;
;
;
;
Ver solução completaSeja um fio retilíneo infinito, paralelo ao eixo , por onde flui uma corrente estacionária . Adjacente a esse fio e a uma distância dele, existe uma espira retangular no plano de lados e , conforme mostra a figura.
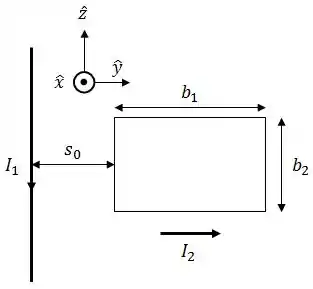
Sabendo-se que a espira carrega uma corrente e que o campo gerado pelo fio é dado (vide formulário), determine:
A força que o fio retilíneo exerce sobre o lado horizontal superior da espira.
A força que o fio retilíneo exerce sobre o lado vertical esquerdo da espira.
A força total sobre a espira (Justifique).
Ver solução completaConsidere uma esfera sólida, de raio R, não condutora e de densidade volumétrica de carga dada por
Concêntrica a essa esfera, temos uma casca esférica, espessa e condutora, em equilíbrio eletrostático, de raio interno e raio externo , onde foi depositada uma carga .
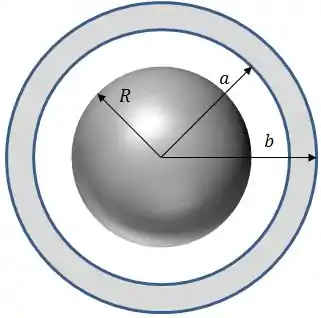
Calcule a carga total da esfera não-condutora.
Calcule o campo elétrico dentro da esfera não-condutora.
Calcule a densidade superficial de carga e nas superfícies interna e externa da casca, e expresse a sua resposta em termos de , , e .
Determine a diferença de potencial entre as superfícies da casca.
Ver solução completaQual é o trabalho necessário para formarmos a configuração das quatro partículas da figura (3 partículas positivas e uma negativa, nos vértices de um quadrado de lado ), supondo que as partículas estejam, de início, infinitamente afastadas umas das outras?
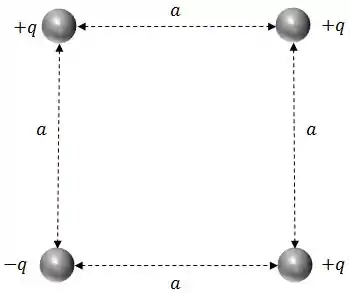
Ver solução completa
Seja uma região delimitada por uma superfície fechada . Tal região possui uma densidade volumar de carga e uma carga total . A partir da lei de Gauss, pode-se dizer que:
Se , o campo elétrico é nulo no interior de .
Se , o campo elétrico é nulo no interior de .
Se , o campo elétrico é nulo em .
Se , o campo elétrico é nulo em .
Nenhuma das opções anteriores.
Ver solução completaUma barra de cobre cilíndrica, de resistência elétrica , comprimento e seção reta , é comprimida para a metade do seu comprimento original, sem que seu volume se altere.
Pode-se afirmar que o novo valor de sua resistência elétrica é:
Ver solução completa
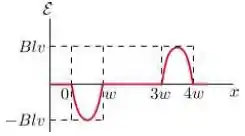
Uma espira condutora retangular de dimensões e se move com velocidade constante para a direita, conforme a figura.
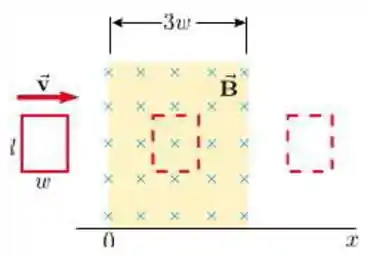
A espira atravessa um campo magnético uniforme e estacionário , dirigido para dentro da página, numa extensão de ao longo do eixo .
Assinale abaixo o gráfico que melhor representa a forca eletromotriz como função da posição da lateral à direita da espira:
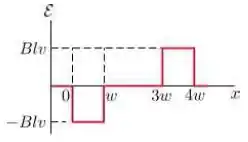
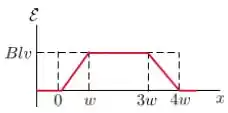
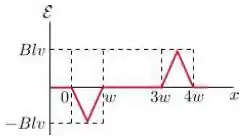
Considere as seguintes afirmações:
- O campo magnético de uma espira circular por onde passa uma corrente estacionária satisfaz a lei de Ampère.
- A afirmação é verdadeira devido à simetria axial da espira.
- Se a espira fosse quadrada, a lei de Ampère não seria válida.
- Se a espira fosse quadrada, a lei de Ampère seria válida, desde que se escolhessem curvas amperiana que passassem pelo centro do quadrado.
São verdadeiras as afirmativas:
Somente
e
, e
e
Somente
Ver solução completa