Introdução ao Campo Elétrico
Considere dois pequenos dipolos elétricos: o primeiro encontra-se no eixo , com seu centro na origem , e é formado por partículas de cargas e , enquanto o segundo encontra-se no eixo e é formado por partículas de cargas e (conforme a figura).
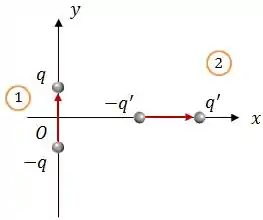
Seja a forca eletrostática exercida pelo dipolo 1 sobre o dipolo 2. Podemos afirmar que:
é nula e o torque sobre o dipolo 1 tende a girá-lo no sentido horário.
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido horário.
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido horário.
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido anti-horário.
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido anti-horário.
Passo 1
Bom, vamos começar desenhando as forças elétricas resultantes sobre cada carga do dipolo 2, beleza?
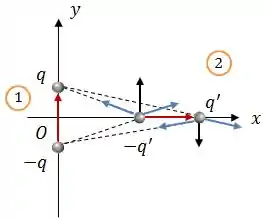
Os vetores azuis representam as forças de interação entre duas partículas e o vetor preto representa a força total sobre cada carga.
Assim, como a carga está mais próxima do dipolo 1 do que a carga , a força tem o sentido de .
Além disso, agora podemos ver que o torque sobre o dipolo 2 tende a girá-lo no sentido horário.
Portanto, a resposta certa é a letra .
Resposta
tem o sentido de e o torque sobre o dipolo 2 tende a girá-lo no sentido horário.