Uma espira condutora retangular de dimensões e se move com velocidade constante para a direita, conforme a figura.
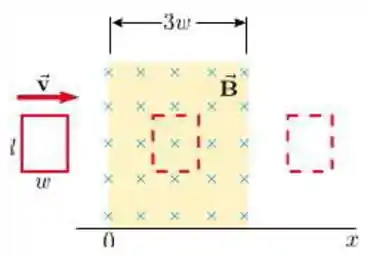
A espira atravessa um campo magnético uniforme e estacionário , dirigido para dentro da página, numa extensão de ao longo do eixo .
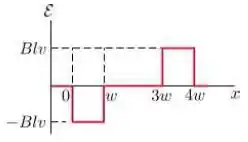
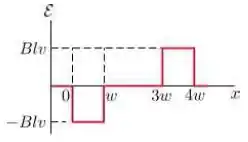
Assinale abaixo o gráfico que melhor representa a forca eletromotriz como função da posição da lateral à direita da espira:
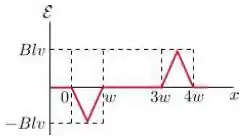
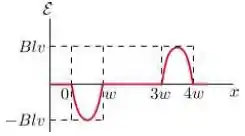
Passo 1
A induzida, de acordo com a lei de Faraday, é dada por:
Então a induzida depende da variação do fluxo magnético.
Assim, quando a espira está totalmente fora da região de fora do campo magnético (, e ) e totalmente dentro da região onde há campo magnético () não há variação do fluxo magnético.
Passo 2
Durante o processo de entrada da espira da região com o campo magnético, a área por onde passa campo magnético através da espira é dada por:
Visto que a área varia conforme a espira entra na região.
A induzida será dada por:
Como a velocidade da espira é constante, temos
Ou seja, no processo de entrada o valor é constante e negativo.
Isso faz total sentido já que ao entrar na região com campo magnético, o fluxo de campo magnético através da espira está aumentando e como resposta a isso, temos uma negativa!
Passo 3
Durante o processo de saída da espira da região com o campo magnético, a área por onde passa campo magnético através da espira é dada por:
Visto que a área varia conforme a espira entra na região.
A induzida será dada por:
Como a velocidade da espira é constante, temos
Ou seja, no processo de saída o valor é constante e positivo.
Isso faz total sentido já que ao sair da região com campo magnético, o fluxo de campo magnético através da espira está diminuindo e como resposta a isso, temos uma positiva!
Portanto, a alternativa que melhor representa a induzida é a letra .
Resposta