Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Ampère

Ver Teoria
Exercício 641234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Força e Torque sobre uma Espira

Seja um fio retilíneo infinito, paralelo ao eixo Z , por onde flui uma corrente estacionária I 1 . Adjacente a esse fio e a uma distância s 0 dele, existe uma espira retangular no plano Y Z de lados b 1 e b 2 , conforme mostra a figura.

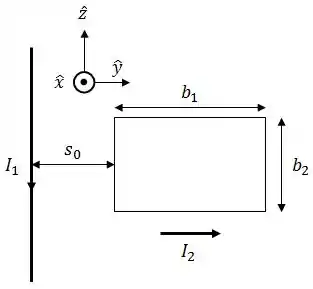
Sabendo-se que a espira carrega uma corrente I 2 e que o campo gerado pelo fio é dado (vide formulário), determine:

a A força que o fio retilíneo exerce sobre o lado horizontal superior da espira.

b A força que o fio retilíneo exerce sobre o lado vertical esquerdo da espira.

c A força total sobre a espira (Justifique).

Passo 1

a A força que o fio retilíneo exerce sobre o lado horizontal superior da espira.

A força magnética sobre um fio condutor é dada por:

F → = ∫ corpo   I   d l → × B →

Primeiro, precisamos descobrir a expressão do campo magnético gerado pelo fio infinito.

De acordo com a lei de Ampère:

∮ C   B → ∙ d l → = μ 0 I i n t

A amperiana aqui é uma circunferência de raio y , logo:

2 π y B y = μ 0 I 1

B y = μ 0 I 1 2 π y

De acordo com a regra da mão direita, na região onde está a espira, o campo magnético terá o sentido do vetor + x ^ , portanto:

B → y = μ 0 I 1 2 π y x ^

Passo 2

O vetor d l → tem a mesma direção e sentido da corrente, logo, ele será dado por:

d l → = - d y y ^

s 0 ≤ y ≤ s 0 + b 1

Logo, a força será dada por:

F → H S = ∫ s 0 s 0 + b 1 I 2 - d y y ^ × μ 0 I 1 2 π y x ^

F → H S = - μ 0 I 1 I 2 2 π ∫ s 0 s 0 + b 1 d y y y ^ × x ^

Onde y ^ × x ^ = - z ^ , logo:

F → H S = μ 0 I 1 I 2 2 π ∫ s 0 s 0 + b 1 d y y z ^

F → H S = μ 0 I 1 I 2 2 π ln ⁡ s 0 + b 1 s 0 z ^

Passo 3

b A força que o fio retilíneo exerce sobre o lado vertical esquerdo da espira.

A diferença agora é que o campo magnético sobre esse fio é constante e, seguindo a mesma lógica do item anterior, vale:

B → = μ 0 I 1 2 π s 0 x ^

Além disso, o vetor d l → agora será:

d l → = - d z z ^

Logo:

F → V E = ∫ f i o I 2 - d z z ^ × μ 0 I 1 2 π s 0 x ^

F → V E = - μ 0 I 1 I 2 2 π s 0 ∫ f i o d z z ^ × x ^

F → V E = - μ 0 I 1 I 2 2 π s 0 ∫ f i o d z y ^

Onde a integral ∫ f i o d z corresponde ao comprimento do fio, sendo assim:

F → V E = - μ 0 I 1 I 2 b 2 2 π s 0 y ^

Passo 4

c A força total sobre a espira (Justifique).

Já temos as forças sobre os fios horizontal superior e vertical esquerdo, dadas por:

F → H S = μ 0 I 1 I 2 2 π ln ⁡ s 0 + b 1 s 0 z ^

F → V E = - μ 0 I 1 I 2 b 2 2 π s 0 y ^

A força total será a soma vetorial das forças sobre cada fio.

F → t o t a l = F → H S + F → H I + F → V E + F → V D

  • F → H I :

    • A única diferença entre essa força e a força sobre o condutor horizontal superior é que agora a corrente está no sentido do vetor + y ^ , assim:

    d l → = d y y ^

    s 0 ≤ y ≤ s 0 + b 1

    Logo, a força será dada por:

    F → H I = ∫ s 0 s 0 + b 1 I 2 d y y ^ × μ 0 I 1 2 π y x ^

    F → H I = μ 0 I 1 I 2 2 π ∫ s 0 s 0 + b 1 d y y y ^ × x ^

    Onde y ^ × x ^ = - z ^ , logo:

    F → H I = - μ 0 I 1 I 2 2 π ∫ s 0 s 0 + b 1 d y y z ^

    F → H I = - μ 0 I 1 I 2 2 π ln ⁡ s 0 + b 1 s 0 z ^

    Passo 5

  • F → V D :

A diferença dessa força para a força sobre o fio vertical esquerdo é que, agora, o campo magnético sobre o fio será dado por:

B → = μ 0 I 1 2 π s 0 + b 1 x ^

Além disso, agora a corrente está no sentido do vetor + z ^ . Assim:

d l → = d z z ^

Logo:

F → V D = ∫ f i o I 2 d z z ^ × μ 0 I 1 2 π s 0 + b 1 x ^

F → V D = μ 0 I 1 I 2 2 π s 0 + b 1 ∫ f i o d z z ^ × x ^

F → V D = μ 0 I 1 I 2 2 π s 0 + b 1 ∫ f i o d z y ^

Onde a integral ∫ f i o d z corresponde ao comprimento do fio, sendo assim:

F → V D = μ 0 I 1 I 2 b 2 2 π s 0 + b 1 y ^

Finalmente, a força total sobre a espira será:

F → t o t a l = F → H S + F → H I + F → V E + F → V D

F → t o t a l = μ 0 I 1 I 2 2 π ln ⁡ s 0 + b 1 s 0 z ^ - μ 0 I 1 I 2 2 π ln ⁡ s 0 + b 1 s 0 z ^ - μ 0 I 1 I 2 b 2 2 π s 0 y ^ + μ 0 I 1 I 2 b 2 2 π s 0 + b 1 y ^

F → t o t a l = - μ 0 I 1 I 2 b 2 2 π s 0 y ^ + μ 0 I 1 I 2 b 2 2 π s 0 + b 1 y ^

F → t o t a l = μ 0 I 1 I 2 b 2 2 π - 1 s 0 + 1 s 0 + b 1 y ^

F → t o t a l = μ 0 I 1 I 2 b 2 2 π - b 1 s 0 s 0 + b 1 y ^

Agora sim!

F → t o t a l = - μ 0 I 1 I 2 b 1 b 2 2 π s 0 s 0 + b 1 y ^

Resposta

a

F → H S = μ 0 I 1 I 2 2 π ln ⁡ s 0 + b 1 s 0 z ^

b

F → V E = - μ 0 I 1 I 2 b 2 2 π s 0 y ^

c

F → t o t a l = - μ 0 I 1 I 2 b 1 b 2 2 π s 0 s 0 + b 1 y ^

Exercícios de Livros Relacionados

41- Um supercondutor do tipo I I em um campo magnético externo entre B c 1 e B c 2 possui regiões supercondutores e regiões com resistência na qual existe campo magnético. Qual é a resistência de um c
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios a e b que conduz uma corrente i uniformemente distribuída. (a) Mostre que, no intervalo bra , o módulo B ( r ) do campo elét
74- Um condutor possui forma de um cilindro oco, sendo a o raio interno e b o raio externo. Ele conduz uma corrente I uniformemente distribuída ao longo da sua seção reta. Deduza expressões para o mód
81- Um plano infinito que conduz uma corrente. Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa
82- Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa fina que se estende até o infinito, sendo