P1 de Física 3 da USP - 2013

Um capacitor esférico é formado por uma esfera interna de raio e uma camada esférica concêntrica de raio interno , conforme a figura.

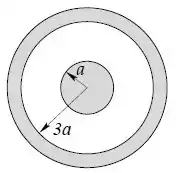
1. Calcule a capacitância deste capacitor no vácuo a partir da definição.
2. Como se altera a capacitância se o espaço entre os condutores for preenchido com um material de constante dielétrica ?
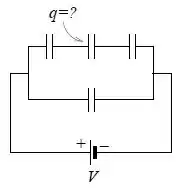
3. Quatro capacitores de capacitância , inicialmente descarregados, foram associados e uma diferença de potencial foi aplicada, conforme a figura. Determine a carga na placa indicada na figura. Dê sua resposta em termos de e .

Uma camada semiesférica isolante de raio interno e externo tem uma densidade volumétrica de carga que decresce com o inverso da distância ao centro segundo .

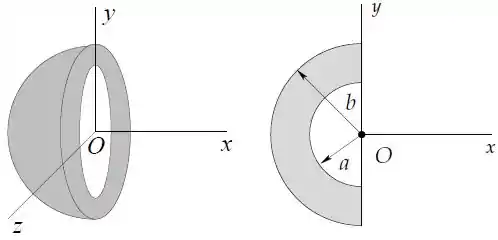
Dados e .

1. Determine a carga total da camada semiesférica.
2. Determine o potencial elétrico no ponto da cama semiesférica. Adote potencial nulo no infinito.
3. Se uma carga pontual com o mesmo sinal da constante da densidade volumétrica de carga é solta no centro , qual é a velocidade final que ela atinge?

Um cilindro circular muito longo de raio , isolante, com densidade volumétrica uniforme de cargas iguais a , é concêntrico a uma camada cilíndrica condutora de raio interno e raio externo com carga total zero.

O campo elétrico no ponto imediatamente fora do condutor vale .

Nos itens abaixo despreze o campo elétrico e as cargas nas extremidades do cilindro e da camada cilíndrica.

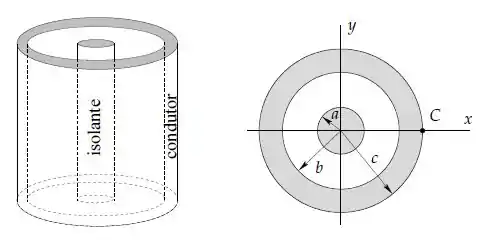
1. Calcule o campo elétrico para e .
2. Calcule o campo elétrico para .
3. Calcule as densidades superficiais de carga e nas superfícies externa e interna da camada cilíndrica condutora em função de , , e .

Considere um bastão de comprimento e carregado com densidade linear uniforme de carga disposto conforme a figura.

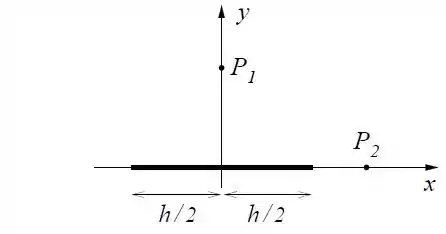
1. Calcule o vetor campo elétrico no ponto de coordenadas , para .
2. Calcule o potencial elétrico no ponto de coordenadas . Para .
3. A partir do potencial calcule a componente do campo elétrico no ponto de coordenadas , para .