Um cilindro circular muito longo de raio , isolante, com densidade volumétrica uniforme de cargas iguais a , é concêntrico a uma camada cilíndrica condutora de raio interno e raio externo com carga total zero.
O campo elétrico no ponto imediatamente fora do condutor vale .
Nos itens abaixo despreze o campo elétrico e as cargas nas extremidades do cilindro e da camada cilíndrica.
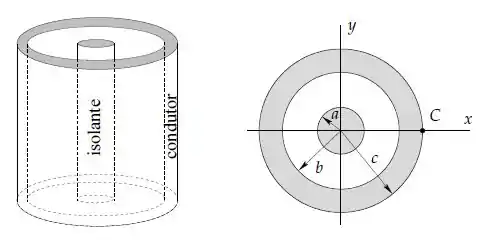
- Calcule o campo elétrico para e .
- Calcule o campo elétrico para .
- Calcule as densidades superficiais de carga e nas superfícies externa e interna da camada cilíndrica condutora em função de , , e .
Passo 1
- Calcule o campo elétrico para e .
Sim, eu sei que você já está pensando nisso... e sim, é o que vamos usar pra resolver o problema... lei de Gauss.
Beleza, antes de começar, vale a pena falar brevemente sobre isolantes e condutores.
Isolantes possuem uma resistência muito alta, , assim, mesmo no equilíbrio eletrostático, as cargas no sem interior continuam com a mesma distribuição, porque a resistência é tão alta que as cargas “não conseguem se reorganizar”.
Condutores possuem uma resistência muito baixa, , isso faz com que, no equilíbrio eletrostático as cargas, nesse caso, vão estar na superfície externa e interna (no caso de uma carga localizada dentro do condutor, como a desse problema) do cilindro. Isso acontece porque, como a resistência é muito pequena “elas conseguem se reorganizar”.
A figura abaixo ilustra o que acontece.
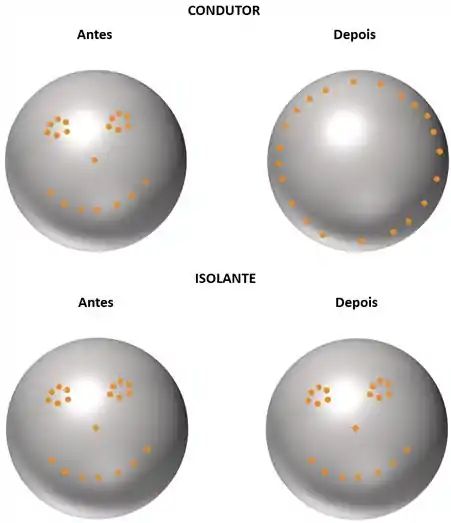
Agora sim, vamos seguir em frente.
Vamos calcular o campo elétrico em cada região separadamente.
Passo 2
- :
- :
Vamos usar a lei de Gauss, nesse caso, a nossa gaussiana vai ser um cilindro de raio e comprimento .
Onda a área é a área lateral da nossa gaussiana e , sendo o volume da nossa gaussiana.
Passo 3
Lá vai uma dica pra você guardar no coração, beleza?
No interior de um condutor, o campo elétrico é sempre igual a zero, no equilíbrio eletrostático.
Logo:
Passo 2
Aqui não tem muito erro, temos apenas que usar a lei de Gauss para sermos felizes.
Agora a nossa gaussiana será um cilindro de raio e comprimento . A área será a área lateral da nossa gaussiana cilíndrica.
A carga interna será a carga do isolante cilíndrico de raio :
Seguindo o mesmo raciocínio que usamos anteriormente:
Passo 3
A definição de densidade superficial de carga é dada por:
Mas se compararmos com a lei de Gauss, vemos que podemos igualar isso aqui com:
Logo:
O problema falou para a gente que na superfície de raio , o campo elétrico , logo:
Passo 4
Bom, já sabemos que a carga total no condutor é nula, certo? Isso significa que:
Novamente, podemos associar a carga com a densidade de carga:
Substituindo na equação anterior:
Agora não tem erro... agora é só substituir o que encontramos no Passo 5.
Resposta
- Para :
Para :