Um capacitor esférico é formado por uma esfera interna de raio e uma camada esférica concêntrica de raio interno , conforme a figura.
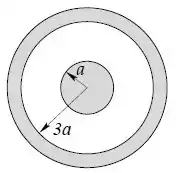
- Calcule a capacitância deste capacitor no vácuo a partir da definição.
- Como se altera a capacitância se o espaço entre os condutores for preenchido com um material de constante dielétrica ?
- Quatro capacitores de capacitância , inicialmente descarregados, foram associados e uma diferença de potencial foi aplicada, conforme a figura. Determine a carga na placa indicada na figura. Dê sua resposta em termos de e .
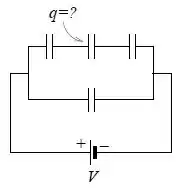
Passo 1
- Calcule a capacitância deste capacitor no vácuo a partir da definição.
- Calcular o campo elétrico na região ;
- Calcular o potencial elétrico na região ;
- Calcular a capacitância;
- Calcular o campo elétrico na região ;
- Calcular o potencial elétrico na região ;
- Calcular a capacitância;
- Como se altera a capacitância se o espaço entre os condutores for preenchido com um material de constante dielétrica ?
- Quatro capacitores de capacitância , inicialmente descarregados, foram associados e uma diferença de potencial foi aplicada, conforme a figura. Determine a carga na placa indicada na figura. Dê sua resposta em termos de e
Vamos lá!
A definição de capacitância diz que:
Aí você olha e pensa: “Beleza! Vou calcular potencial entre as duas superfícies esféricas, de raios e !”. Boa! O caminho é esse mesmo!
Mas por definição, o potencial elétrico é dado por:
Opa! Então temos que começar calculando o campo elétrico no interior do capacitor esférico!
Então lá vai a ordem das coisas que temos que fazer:
Passo 2
Pra isso, vamos utilizar a lei de Gauss... não tem muito mistério.
A nossa gaussiana será a esfera de raio . Lei de Gauss neles!
Passo 3
Passo 4
Passo 5
Esse aqui é ponto ganho pra você que sabe o que é um material dielétrico. Na dúvida, qualquer coisa dá uma lida no nosso material pra ficar mais tranquilo.
De qualquer forma, quando adicionamos um material dielétrico entre os terminais de um capacitor, a capacitância agora será dada por:
É isso.
Passo 6
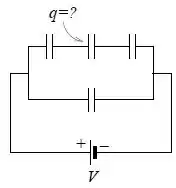
Beleza! Pra começar, temos 3 capacitores em paralelo com um outro capacitor. Já que temos esses caras em paralelo, a diferença de potencial tanto no ramo de cima, quanto no ramo de baixo, será igual a . Até aqui, nenhum mistério.
A segunda coisa que você precisa lembrar é que quando os capacitores são colocados em série, todos eles possuem a mesma carga .
Sendo assim:
Onde é a diferença de potencial em cada um dos capacitores.
Pronto! Sem drama, né?