Considere um fio retilíneo muito longo de raio e centrado ao longo do eixo no qual passa uma corrente estacionária (ao longo da direção ), conforme mostra a figura abaixo. A corrente elétrica é distribuída de forma que sua densidade de corrente é dada por: (se ), e caso contrário, sendo uma constante.
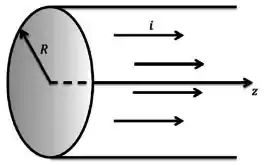
- Determine a corrente total em função de e .
- Usando a lei de Ampère, encontre o vetor campo magnético na região .
- Usando a lei de Ampère, encontre o vetor magnético na região .
Passo 1
a) Precisamos nos lembrar aqui que o elemento de corrente atravessando o elemento de área relaciona-se com a densidade de corrente de acordo com
que é o produto escalar dos vetores e . A direção e sentido de o problema já deu para gente e agora temos que ver como fica . Para isso, vamos olhar a figura abaixo, que mostra o desenho do perfil do cilindro acima.
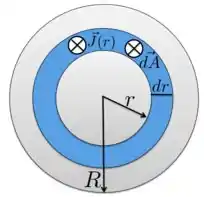
Nessa figura, colocamos vetor saindo do plano da página na mesma direção e sentido de , ou seja, . Portanto, nesse caso temos que a corrente total é:
Passo 2
b) A corrente dentro da região produz um campo magnético que é sempre tangente a qualquer curva fechada centrada no eixo . A direção e sentido do campo magnético é dada pelo vetor unitário , como mostra a figura abaixo.
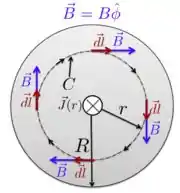
Como colocamos na figura, a nossa amperiana, ou seja, a nossa curva fechada , é um círculo de raio que está orientado no sentido horário. Por isso, o campo magnético é sempre paralelo ao vetor elemento de comprimento da amperiana.
Além disso, depende da distância ao eixo , mas tem o mesmo valor em todos os pontos sobre a amperiana. Por isso, o lado esquerdo da lei de Ampère pode ser escrito como:
Agora, para calcular o lado direito da lei de Ampère (), precisamos ter mais cuidado, porque através da área definida pela amperiana de raio passa apenas uma parte da corrente total . Para encontrar essa corrente, a gente tem que fazer a seguinte conta:
Em outras palavras, é repetir os passos do item a) só que tomando o cuidado com os limites de integração! Ok?
Se fazemos isso, teremos o seguinte:
que é a corrente que passa através da área definida pela curva amperiana. Fechou?? Fica ligado nesse tipo de ideia, porque costuma cair bastante nessa parte... ;-).
Para matar essa parte, vamos juntar tudo:
Portanto, o vetor campo magnético é escrito como:
Passo 3
c) O lado esquerdo da lei de Ampère continua o mesmo que no item anterior: . Para termos o lado direito, agora vamos olhar para uma amperiana que tem raio .
Nesse caso, a área da amperiana é atravessada por toda a corrente . Por isso, teremos o seguinte:
Por isso, o vetor campo magnético é dado por: