Um material condutor de condutividade uniforme tem o formato de um semi-círculo de altura e raios e , conforme indicado nas figuras e , respectivamente. As superfícies localizadas em e são equipotenciais e mantidas a uma diferença de potencial por uma bateria. Vamos assumir que o potencial elétrico dentro do condutor depende somente da coordenada , de forma que os efeitos de borda podem ser desprezados.
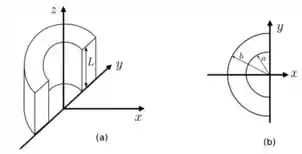
- A bateria fornece uma corrente elétrica . Assumindo a conservação de corrente, determine o vetor densidade de corrente .
- Determine o campo elétrico no interior do condutor.
- Calcule a resistência do condutor em função de sua condutividade e de suas dimensões.
Passo 1
a) Para resolvermos este item, precisamos entender bem qual área a corrente está atravessando. Para isso, imagine que você está em pé sobre o eixo e olhando para o plano no sentido de , como mostrado na figura da esquerda abaixo.
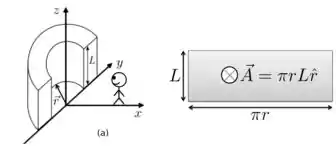
A área que você vai ver a corrente atravessar é a que está mostrada à direita, cujo vetor área é dado por:
Como o vetor densidade de corrente vai estar ao longo da direção , podemos escrever:
Passo 2
b) Se o material condutor da questão obedece a lei de Ohm, então vale que . Nesse caso, o campo elétrico será:
Passo 3
c) Para encontrarmos a resistência do condutor, precisamos encontrar a ddp entre os pontos e . Para calcular , podemos fazer o seguinte cálculo:
Como o campo elétrico está na direção e sentido de , podemos considerar também , ou seja, é paralelo a . Colocando essa informação junto com a expressão para que encontramos no Passo 2 dentro de , teremos:
Agora, como a resistência é dada por , temos, a partir da expressão acima, que seu valor é: