Um circuito condutor é composto por dois fios retilíneos semi-infinitos e uma parte circular, representados pelas linhas escuras, conforme mostrado na figura abaixo. Ele está contido no plano e conduz uma corrente no sentido indicado. Para e os trechos são retilíneos (fios semi-infinitos). Para e , o condutor tem a forme de três quartos de circunferência com raio .
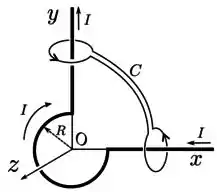
- Calcule o vetor campo magnético na origem devido aos segmentos lineares do fio.
- Calcule o vetor campo magnético na origem do sistema de coordenadas devido à parte circular.
- Determine o valor da integral ao longo do percurso indicado na figura.
Passo 1
a) Para resolvermos este item, considere a figura abaixo, em que só temos os segmentos lineares.
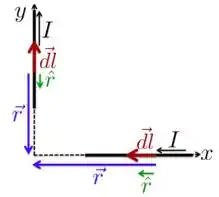
Os vetores , que representam os elementos de comprimento, sempre estão na direção e sentido da corrente que passa no condutor. O vetor unitário e o vetor distância sempre são orientados partindo de em direção ao ponto onde queremos calcular o campo produzido por . Dá uma olhada na figura acima e guarda isso, porque é muito importante para a utilização da lei de Biot-Savart.
A lei de Biot-Savart diz que o campo magnético produzido por uma corrente passando por elemento de um condutor é dada por:
Agora, no condutor que está sobre o eixo da figura, o vetores e são antiparalelos, ou seja, o ângulo entre eles é de . Portanto, . Como todos os elementos desse condutor estão antiparalelos a , o campo produzido pela corrente nesse condutor é nulo no ponto .
Já no condutor sobre o eixo , esses vetores são paralelos e também teremos . Da mesma maneira, esse condutor não produz campo sobre o ponto . Por isso, o campo total no ponto devido a esses segmentos é:
Passo 2
b) Já nesse caso do segmento circular, precisamos olhar com mais calma o produto vetorial . Para isso, vamos usar a figura abaixo, em que representamos cada um desses vetores.
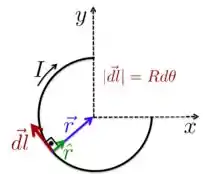
Nesse caso, o vetor é tangente em todos os pontos do condutor e, por essa razão, é também sempre perpendicular ao vetor unitário que aponta para o ponto em que queremos o campo magnético. Por isso, temos que
Além disso, o vetor , que aponta na direção e sentido de , tem o mesmo módulo em todos os pontos do condutor, já que estão à mesma distância do ponto . Então, podemos representá-lo como: .
Juntando essas informações dentro da lei de Biot-Savart, teremos:
que simplificada, fica:
Passo 3
c) A lei de Ampère estabelece que:
em que é a corrente que atravessa a área definida pela curva fechada . Na figura, as correntes que atravessam área dessa curva são tem mesmo módulo, mas sentidos contrários, o que dá para gente o seguinte:
Por isso, a circulação do campo magnético, ou a integral de linha do campo magnético, ao longo de é dada por: