P2 de Física 4 da USP - 2017

Uma partícula instável, de massa de repouso , inicialmente em repouso, decai produzindo duas partículas idênticas. Suponha que a massa de repouso e a energia cinética K de cada uma das partículas finais sejam conhecidas. Considere também que o sistema permanece isolado ao longo de todo o processo.

(a) Seja v a velocidade de uma das partículas de massa de repouso . Calcule v/c, onde c é a velocidade da luz no vácuo. Expresse sua resposta em termos de, K e c.

(b) Calcule o valor da massa , expressando sua resposta em termos de , K e c.

(c) Determine v, quando = 0.

Um fóton de comprimento de onda incide sobre um elétron em repouso que possui massa de repouso igual a , conforme a figura. Após o espalhamento, o fóton adquire um comprimento de onda λ’ e é espalhado de um ângulo de 90° em relação ao eixo x (direção de incidência) e o elétron se move com momento de módulo P, formando um ângulo em relação ao eixo x. Expresse os resultados apenas em termos de h, c, e .

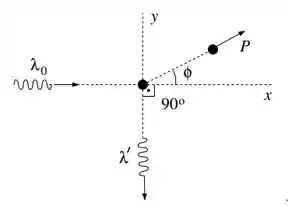
(a) Qual é o comprimento de onda λ’ do fóton espalhado?

(b) Determine a energia cinética do elétron após o espalhamento.

(c) Calcule o vetor momento linear do elétron após o espalhamento.

Um feixe de luz de comprimento de onda λ e intensidade I, incide sobre uma placa de área A, no interior de uma célula fotoelétrica. O material da placa possui função trabalho .

(a) Calcule e energia e o módulo do momento dos fótons incidentes.

(b) Calcule o número N de fótons incidentes sobre a placa em um intervalo de tempo ∆t.

(c) Determine a condição que deve ser satisfeita pelo valor de λ para que sejam ejetados elétrons do material.

Uma estrela esférica de raio R em equilíbrio térmico à temperatura T emite radiação térmica.

(a) Supondo que a estrela emita energia térmica como um corpo negro, calcule a quantidade de massa ∆m perdida pela estrela durante um intervalo de tempo ∆t.

(b) Um laboratório na Terra observa que o comprimento de onda do máximo da distribuição de radiação térmica da estrela é . Supondo que a estrela esteja se afastando da Terra com velocidade v = 0, 6c, calcule sua temperatura.

Um átomo de hidrogênio possui um elétron na camada n = 2.

(a) Calcule o comprimento de onda do fóton emitido quando este elétron faz uma transição da camada n = 2 para a camada n = 1

(b) Determine a energia mínima de um fóton incidente para remover um elétron da camada n=2 do átomo de hidrogênio (Esta é a energia para ionizar o átomo de hidrogênio com o elétron neste nível excitado.).