Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Espalhamento Compton

Ver Teoria
Exercício 4212345678910111213141516171819202122232425262728293031323334353637383940414344454647

Enunciado

PUC, Física 4, P1 2017.2, 2

Um fóton de comprimento de onda λ 0 incide sobre um elétron em repouso que possui massa de repouso igual a m 0 , conforme a figura. Após o espalhamento, o fóton adquire um comprimento de onda λ’ e é espalhado de um ângulo de 90° em relação ao eixo x (direção de incidência) e o elétron se move com momento de módulo P, formando um ângulo ∅ ≠ 0 em relação ao eixo x. Expresse os resultados apenas em termos de h, c, λ 0 e m 0 .

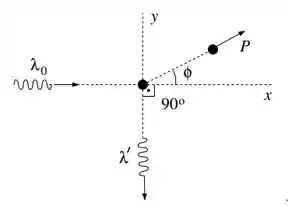
(a) Qual é o comprimento de onda λ’ do fóton espalhado?

(b) Determine a energia cinética do elétron após o espalhamento.

(c) Calcule o vetor momento linear do elétron após o espalhamento.

Passo 1

Antes de qualquer coisa vamos relembrar a fórmula de Compton para o espalhamento de um fóton, a fórmula é a seguinte

λ ’ - λ 0 = λ c o m p t o n . ( 1 - c o s θ )

em que cada termo dessa fórmula representa

λ ’ = c o m p r i m e n t o   d e   o n d a   d o   f ó t o n   a p o s   o   e s p a l h a m e n t o  

λ 0 = c o m p r i m e n t o   d e   o n d a   d o   f ó t o n   a n t e s   d o   e s p a l h a m e n t o  

θ = â n g u l o   e m   q u e   o c o r r e u   o   e s p a l h a m e n t o  

E por fim

λ c o m p t o n = c o m p r i m e n t o   d e   o n d a   d e   c o m p t o n ,   d a d o   p e l a   f ó r m u l a  

λ c o m p t o n = h m 0 . c

Como o nosso objetivo é determinar o valor de λ ’ vamos isola-lo na fórmula

λ ’ = λ 0 + λ c o m p t o n . ( 1 - c o s θ )

pela imagem podemos ver claramente que o espalhamento do nosso fóton ocorreu segundo um ângulo de 90°, o que também foi dito no nosso enunciado, dessa forma se fizemos a substituição teremos,

λ ’ = λ 0 + λ c o m p t o n . ( 1 - c o s 90 ° )

λ ’ = λ 0 + λ c o m p t o n

e já sabemos quanto vale o λ c o m p t o n , substituindo teremos,

λ ’ = λ 0 + h m 0 . c

Passo 2

O nosso segundo objetivo é determinar a energia cinética no elétron, e sabemos que para o elétron a fórmula da sua energia relativística será dada por

E e = K + m 0 . c 2  

Lembrando que um componente é da energia cinética e a outra é da energia de repouso do elétron.

Mas ainda sim não conseguimos determinar a energia cinética no elétron, para isso temos que lembrar de outra coisa bem simples, o fóton quando chega no elétron possui uma energia que após o espalhamento passa a funcionar de maneira diferente, e como assim diferente?

Pensa na conservação de energia, a energia do fóton que chega mais a energia de repouso do elétron deve ser igual a energia do fóton que espalha mais a energia absorvida pelo elétron, ou seja, podemos escrever a fórmula da seguinte maneira, lembrando que para o fóton a sua energia é dada pela fórmula E f = h . f = h . c λ .

E   a n t e s = E   d e p o i s + E e  

Ou seja, podemos dizer que

E e = E   a n t e s - E   d e p o i s

E sabemos como calcular a energia do fóton

E e = ( h . c λ 0 + m 0 . c 2 ) - h . c λ ’

Igualando as fórmulas de energia do elétron teremos

( h . c λ 0 + m 0 . c 2 ) - h . c λ ’ = K + m 0 . c 2

Podemos então cortar o valor de m 0 . c 2 de ambos os lados e teremos por fim

h . c λ 0 - h . c λ ’ = K

Lembra que no item a calculamos o valor de λ ’ ? vamos então substitui-lo na nossa equação e definir a fórmula para energia cinética do nosso elétron.

K = h . c λ 0 - h . c λ 0 + h m 0 . c

Passo 3

Por fim, nos é pedido para calcularmos o valor do vetor momento linear do nosso elétron.

Para isso precisamos relembrar que Compton definiu que o momento linear do fóton pode ser definido como.

p = h λ

Mas perceba que nesse caso ocorrer a conservação de momento linear, ou seja, se isso acontece significa que podemos analisar cada eixo separadamente e a partir dele definir a conservação do momento linear.

Então sabemos que antes do espalhamento o fóton possui o seguinte momento linear.

p x = h λ 0

Lembrando que esse momento linear é definido exatamente por sabermos que o fóton estava se propagando na direção x antes do espalhamento. Posteriormente vemos que ele passa a se propagar na direção y, ou seja, podemos escrever que o momento linear nessa direção também se conserva, fazendo isso teremos,

p y = h λ ’

Feito isso podemos dizer que o vetor momento linear do elétron conserva cada eixo de momento linear do fóton, o que significa que podemos escrever o vetor momento linear do elétron da seguinte forma,

p → = p x . i ^ + p y . j ^

Substituindo teremos

p → = h λ 0 . i ^ + h λ ’ . j ^

Fazendo ainda a substituição de λ ’ teremos

p → = h λ 0 . i ^ + h λ 0 + h m 0 . c . j ^

Resposta

a) λ ’ = λ 0 + h m 0 . c

b) K = h . c λ 0 - h . c λ 0 + h m 0 . c

c) p → = h λ 0 . i ^ + h λ 0 + h m 0 . c . j ^

Exercícios de Livros Relacionados

Um fóton incidente de energia Ei sofre espalhamento de Compton no ângulo de θ. Mostre que a energia Es do fóton espalhado é dada por E s = E i 1 + E i m e c 2 1 - cos ⁡ θ
Quando os fótons são dispersos por elétrons em uma amostra de carbono, a mudança no comprimento de onda é de 0,33 pm. Encontre o ângulo de dispersão. (Suponha que os elétrons estejam se movendo inicia
Durante um laboratório de física avançada, os alunos usam raios X para medir o comprimento de onda de Compton, λC. Os alunos obtêm os seguintes desvios de comprimento de onda λ2 - λ1 em função do ângu
Encontre a mudança no comprimento de onda dos fótons dispersos por elétrons estacionários livres em θ = 60 °. (Suponha que os elétrons estejam se movendo inicialmente a uma velocidade desprezível e es
Os fótons em um feixe monocromático são espalhados por elétrons. O comprimento de onda dos fótons dispersos em um ângulo de 135 ° com a direção do feixe de fótons incidentes é 2,3% menor que o comprim