. Uma partícula de massa se move em uma dimensão na presença de um poço de potencial
de profundidade e largura conforme a figura abaixo. A partícula se encontra num estado estacionário de energia .
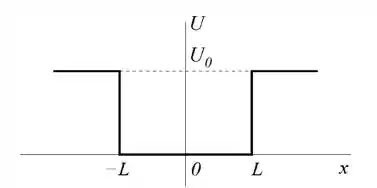
(a) Escreva a equação de Schrödinger independente do tempo desta partícula para e sua solução geral.
(b) Escreva a equação de Schrödinger independente do tempo desta partícula para e e sua solução geral. Qual solução é fisicamente aceitável?
(c) Encontre as condições de contorno que as constantes arbitrárias introduzidas nos itens e devem satisfazer (não é necessário resolver o sistema).
(d) Calcule a probabilidade de encontrar a partícula na região como
função dessas constantes.
Passo 1
Então galera, vamos nos livrar dessa questão com categoria.
A informação principal para resolver essa questão é a equação de Schrödinger independente do tempo mais geral, dada por:
Tendo essa equação basta analisarmos o que cada item quer e ir fazendo as alterações necessárias.
Para facilitar nossa vida, vamos dar nome as coisas. A região onde vamos chamar de região , onde de região e onde de região .
Vamos lá então!
Passo 2
Começando com o item .
Ele quer a equação de Schrödinger na região , só que nessa região temos , logo nossa equação fica assim:
Agora para encontrar a solução geral, temos que mexer um pouco na nossa equação para ela ficar com uma cara melhor.
Podemos dividir toda equação por , assim temos:
Fazendo
Ficamos com:
Bem dizer encontramos uma equação diferencial de segunda ordem. Esse tipo de equação já tem um resultado tabelado dado por:
Prontinho, conseguimos tudo que o item pede.
Passo 3
Agora vamos para o item .
Ele quer a equação de Schrödinger na região e , mas essas regiões estão submetidas ao mesmo potencial , logo nossa equação fica assim:
Agora para encontrar a solução geral, primeiro vamos encontrar a solução geral sem levar em conta se é maior ou menor que ou e depois vamos ver cada região.
Temos que mexer um pouco na nossa equação para ela ficar com uma cara melhor.
Podemos dividir toda equação por , assim temos:
O fato de ter deixado e não , foi porque o enunciado fala que , assim a subtração entre eles fica positiva.
Fazendo
Ficamos com:
Bem dizer encontramos uma equação diferencial de segunda ordem. Esse tipo de equação já tem um resultado tabelado dado por:
Passo 4
Agora vamos olhar as regiões separadamente.
Primeiro vamos analisar a região .
Quando temos temos um problema, o termo da nossa solução diverge e as soluções da equação de Schrödinger não podem divergir.
E lembrando do fato de que em regiões onde a função de onda deve ir a zero, temos que tem quer ser igual zero.
Assim a solução para essa região é:
Agora para a região .
O argumento é bem parecido com o da região , só que agora quando o termo diverge, logo e temos a seguinte solução:
Passo 5
Agora vamos para o item .
Ele quer saber as condições de contorno desse sistema, para achá-las temos que lembrar que a função de onda deve ser continua em qualquer ponto, inclusive nas paredes do poço de potencial.
Isso quer dizer que em , temos que:
E que em , temos que:
Então temos que abrir essas expressões.
Para , temos:
Como cosseno é uma função par e seno é uma função ímpar, temos:
Agora para , temos:
Prontinho, encontramos as condições pedidas.
Passo 6
Agora vamos resolver o item , finalmente o último kkkk.
Ele quer a probabilidade de encontrar a partícula na região . Isso é bem dizer o mesmo que a probabilidade de encontrarmos a partícula na região ou na região .
A probabilidade de encontrarmos a partícula em uma região do espaço é dada pela seguinte equação:
Para o nosso caso ficamos com o seguinte:
Substituindo com o que sabemos, temos:
Passo 7
Agora vamos resolver essas integrais.
Vamos começar com a primeira, temos:
Agora a segunda integral, temos:
Então temos que:
Resposta
Demonstrado acima.