Um passageiro de massa sentado em uma roda gigante se move com velocidade constante em uma trajetória circular de raio no plano vertical no sentido horário. Suponha que durante todo o movimento o passageiro está sempre sentado de cabeça para cima.
a) Faça um diagrama de corpo livre das forças que agem no passageiro no topo e no fundo da trajetória.
b) Escreva uma expressão literal para a diferença das forças normais que agem no passageiro nas duas posições. Como varia esta diferença em função da velocidade da roda gigante?
c) Suponha agora que no instante em que o passageiro alcança sua altura máxima, a força que age no assento aponta para baixo na direção vertical e tem módulo igual à do peso do passageiro. Para um raio igual a , calcule em quanto tempo a roda gigante dá uma volta completa.
Passo 1
(a)
As forças que atuam no passageiro são as forças normais e peso, o que muda do topo para o fundo é apenas a intensidade das forças, pois a resultante tem que estar sempre apontando para o centro da roda gigante, pois será a força centrípeta.
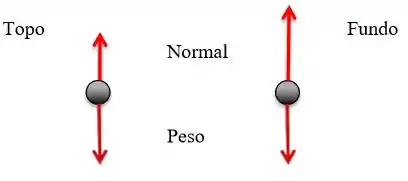
Passo 2
(b)
Basta utilizar a fórmula :
No topo:
No fundo:
A diferença das forças normais varia com o quadrado da velocidade.
Passo 3
(c)
A força que age no acento para baixo é par ação reação da força que o banco faz no passageiro, que é justamente a força normal. Portanto, No topo:
Utilizando a Formula
Substituindo pelo comprimento da roda gigante que é :
Resposta
(a) 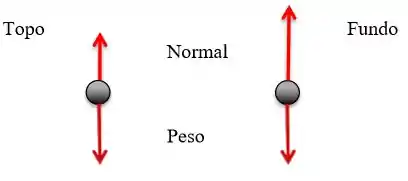
(b) , varia com o quadrado da velocidade.
(c)