Considere a situação ilustrada abaixo onde os dois blocos estão ligados por uma corda que passa por uma polia. O bloco 1 tem massa e o bloco 2 tem massa . As massas da polia e da corda podem ser consideradas como sendo desprezíveis. Existe atrito em todas as superfícies e o coeficiente de atrito cinético é igual a 0,40. Uma força é aplicada no bloco 1 de tal forma que os blocos se deslocam com velocidade constante, o bloco 1 para à direita e o bloco 2 para à esquerda.
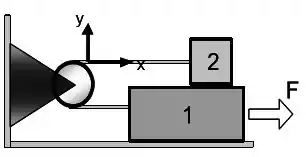
a) Faça o diagrama de corpo livre para o sistema e indique nos dois blocos, se existirem, as forças que formam pares ação-reação.
b) Escreva, na forma literal, as equações de movimento para o sistema. Resolva o sistema de equações e substitua os valores do enunciado para encontrar o vetor força . Utilize o sistema de coordenadas indicado.
Passo 1
(a)
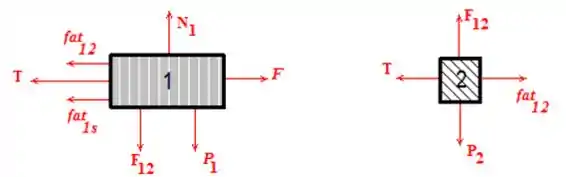
Onde representa a força de atrito entre os dois blocos que irá atuar em ambos. E é a força de atrito do bloco 1 com o solo. Além de que é a força de normal de contato entre os dois blocos.
Há três conjutos de forças em par ação e reação:
1 – força de atrito tangencial entre as superfícies do blocos 1 e 2 ()
2 – tração no fio ideal ()
3 – Força normal entre as superfícies dos blocos 1 e 2 ()
Passo 2
(b)
Aplicando a segunda lei de Newton para cada um dos dois blocos:
Bloco 1:
Bloco 2:
Como os blocos não se movem na vertical, então . Logo:
Usando a (eq.4):
Usando a (eq.2):
Entretanto, descobrimos que , então podemos substituir:
Como os blocos se movem com velocidade constante, . Desta forma:
Usando a (eq.3):
Usando a (eq.1):
Mas já sabemos que então:
Utilizando a fórmula da força de atrito:
Substituindo os valores que encontramos na eq. 2 e eq. 4:
Substituindo os dados:
Resposta
(a) 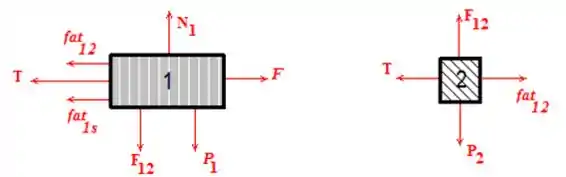
,,
(b)