Três blocos de massa , e estão conectados por cordas ideais através de uma polia ideal, apoiados em superfícies inclinadas de ângulos e como mostrado na figura. As massas dos blocos valem , , , , , e . Os valores dos coeficientes de atrito estático e cinético entre o bloco 1 e seu plano inclinado são respectivamente e .
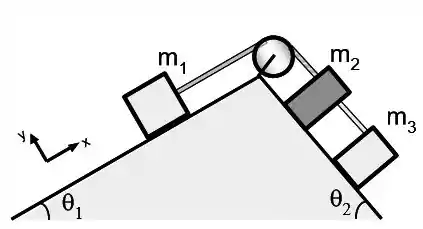
a) Faça um diagrama de corpo livre de cada bloco no espaço abaixo. Usando as leis de Newton, determine o valor da força de atrito estático sobre o bloco 1 para que o sistema permaneça em repouso. Não existe atrito entre os blocos 2 e 3 e o plano inclinado no qual estão apoiados.
b) Considere agora que o bloco 3 sofra a ação de uma força para baixo paralela ao plano inclinado que põe o sistema em movimento. Após certo momento, a ação dessa força cessa. Nesse instante o sistema de blocos está descendo o plano inclinado com velocidade de módulo . A partir desse instante obtenha o valor da aceleração do bloco 1.
c) Calcule a força de tração da corda sobre o bloco 1 durante a aceleração do ítem ().
Passo 1
(a)
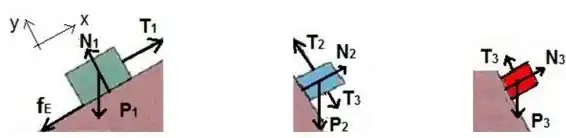
Decompondo as forças peso:
Essa diferença de forças indica que a força de atrito estática sobre o bloco 1 aponta para baixo ao longo do plano inclinado , no mesmo sentido de , para poder compensar as forças e manter o sistema em equilíbrio.
O valor da força de atrito estática máxima é dado por:
Façamos a análise da situação utilizando a segunda lei de Newton mas lembrando que o sistema está em equilíbrio, então a aceleração é nula.
Bloco 1:
Eixo :
Eixo :
Bloco 2:
Eixo :
Eixo :
Bloco 3:
Eixo :
Eixo :
Lembrando que:, , e podemos somar os lados esquerdos dessas equações e igualar à soma dos lados direitos:
Como a força de atrito estática sobre o bloco 1 é .
Passo 2
(b)
Como o sistema desce sobre o plano inclinado o bloco 1 sobe deslizando sobre o seu plano inclinado. Nesse caso a força de atrito cinética sobre esse bloco 1 aponta para baixo ao longo do plano inclinado .
Fazendo novamente a análise da segunda lei de Newton para os blocos:
Bloco 1:
Eixo :
Eixo :
Bloco 2:
Eixo :
Eixo :
Bloco 3:
Eixo :
Eixo :
Lembrando que , , , , (pois os fios são inextensíveis) e , podemos somar os lados esquerdos dessas equações e igualar à soma dos lados direitos:
Passo 3
(c)
Substituindo a aceleração na equação que encontramos para o bloco 1:
Bloco 1:
Eixo :
Eixo :
Substituindo todos os dados:
Resposta
(a) 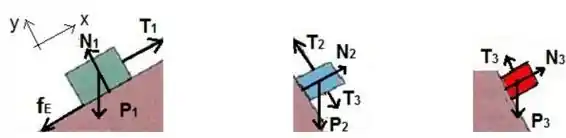
(b)
(c)