P2 de Física B - FIS1026 da PUCRIO - 2013.2

Um automóvel de massa é conduzido em um declive de a uma velocidade de quando acontece um defeito com suas rodas e elas travam. Ele passa então a deslizar sob a ação de uma força de atrito constante de que causa uma parada total do veículo.

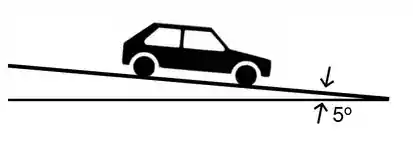
Dados: ; ; ;

Determine a aceleração do automóvel.

Determine o trabalho realizado pela força gravitacional.

Determine trabalho do atrito.

De acordo com seus resultados anteriores diga se foi possível confirmar, para a situação apresentada, a validade do teorema do trabalho e da energia cinética? Justifique.

Uma partícula de massa se move sob a ação de várias forças conservativas e de uma força não conservativa. A energia potencial total em Joules associada às forças conservativas em função da posição em metros é dada pelo gráfico abaixo. Na posição a velocidade da partícula é . No trecho entre e , a força não conservativa realiza trabalho de .

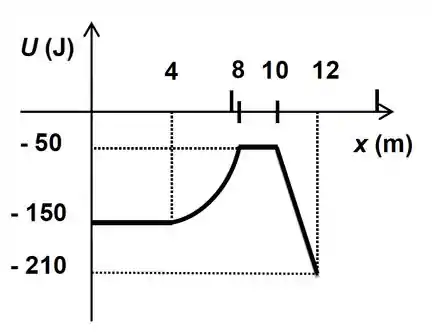
Obtenha a velocidade da partícula em .

Um automóvel de massa inicia em um piso horizontal, a partir do repouso, a subida de uma rampa, cuja altura vertical final é . Ao chegar ao topo da rampa sua energia cinética é igual a . Neste instante, um defeito de travamento das rodas ocorre e o automóvel inicia uma descida, deslizando por outra rampa, até chegar ao nível horizontal. Nesse deslizamento a perda para o meio externo é de de sua energia mecânica no topo. Ao chegar ao nível horizontal ainda com velocidade, o automóvel colide com uma mola horizontal estática comprimindo-a até parar. A mola possui constante elástica , estando com uma extremidade livre e outra presa em uma parede. Na região onde está a mola o piso é rugoso com coeficiente de atrito cinético .

Obs.: Em todos os itens abaixo explicite a razão pela qual é válida a lei física aplicada. Resolva primeiro literalmente. Somente depois faça a aplicação numérica quando for o caso. Considere .

Obtenha uma expressão, em função dos dados conhecidos, para o valor de energia gasto pelo automóvel durante a subida da rampa. Assuma de eficiência do motor. Calcule seu valor numérico.

Encontre uma expressão literal para o valor da velocidade do automóvel ao terminar a descida da rampa. Calcule seu valor numérico.

Deduza uma equação algébrica quadrática para a deformaçãoo máxima da mola em termos dos dados literais fornecidos ( e ).

Considere uma colisão perfeitamente inelástica entre dois automóveis de mesma altura e mesmo comprimento . O automóvel tem massa e velocidade de módulo imediatamente antes de colidir com o automóvel que tem massa e está em repouso. A colisão se dá em um intervalo de tempo muito curto. Considere o sistema de coordenadas indicado na figura. Assuma que o centro de massa de cada automóvel está à meia altura e na metade de seu comprimento.

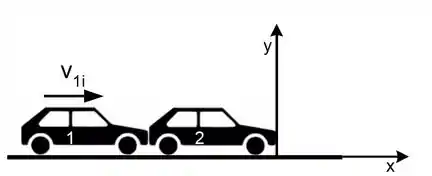
Determine o vetor posição do centro de massa do sistema (dois automóveis) no instante imediatamente antes da colisão.

Determine o vetor velocidade dos destroços imediatamente depois da colisão.

Encontre a expressão literal para a perda de energia cinética durante a colisão. Analise o resultado se .