Energia Potencial e Conservação da Energia Mecânica
Uma partícula de massa se move sob a ação de várias forças conservativas e de uma força não conservativa. A energia potencial total em Joules associada às forças conservativas em função da posição em metros é dada pelo gráfico abaixo. Na posição a velocidade da partícula é . No trecho entre e , a força não conservativa realiza trabalho de .
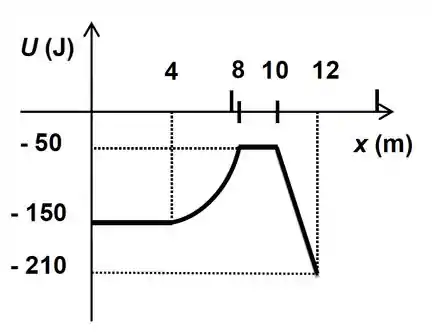
Obtenha a velocidade da partícula em .
Passo 1
Para determinar a velocidade em , tendo em vista que estamos lidando puramente com energia, e pelo fato de termos uma força não conservativa, iremos utilizar a relação entre o trabalho realizado por essa força conservativa e a variação da energia mecânica:
Como precisamos encontrar velocidade em , e ele nos diz o trabalho realizado pela força não conservativa, entre e , . Podemos usar a fórmula citada da seguinte forma:
Passo 2
Pelo gráfico podemos determinar a variação da energia potencial entre esses pontos, dá uma olhada!
Passo 3
Voltando à fórmula do passo , temos:
Substituindo os valores, fica:
Isolando a velocidade, temos:
Resposta