Considere uma colisão perfeitamente inelástica entre dois automóveis de mesma altura e mesmo comprimento . O automóvel tem massa e velocidade de módulo imediatamente antes de colidir com o automóvel que tem massa e está em repouso. A colisão se dá em um intervalo de tempo muito curto. Considere o sistema de coordenadas indicado na figura. Assuma que o centro de massa de cada automóvel está à meia altura e na metade de seu comprimento.

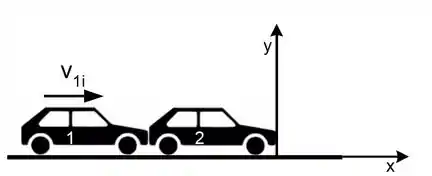
Determine o vetor posição do centro de massa do sistema (dois automóveis) no instante imediatamente antes da colisão.

Determine o vetor velocidade dos destroços imediatamente depois da colisão.

Encontre a expressão literal para a perda de energia cinética durante a colisão. Analise o resultado se .

Em uma colisão, onde não existem forças externas ao sistema atuando, podemos sempre utilizar a conservação do momento linear. Além disso, o enunciado nos dá uma informação muito importante. Ele diz que a colisão é perfeitamente inelástica, isso significa dizer que os corpos vão ter a mesma velocidade final, ou seja, vão sair juntos. Se liga!

antes da colisão, o automóvel está parado e o tem velocidade em módulo. Montando as equações, temos:

Repare que estamos usando a notação vetorial, pois ele nos pede o vetor velocidade final. Pelo vetor desenhado no gráfico, fica claro que sua direção e sentido é dada por . Voltando à equação, temos:

Para analisar a perda da energia cinética, precisamos calcular a variação da energia cinética do sistema antes e depois da colisão. Então, vamos lá:

Parece muito confuso, mas é só lembrar que a velocidade inicial do automóvel é zero, e como já calculamos a velocidade final, é só substituir:

Agora vamos analisar o caso em que :

Podemos ver, nesse caso, que a perda de energia cinética é a metade da energia cinética inicial, pois: