Trabalho e Energia Cinética, Energia Potencial e Conservação da Energia Mecânica
Um automóvel de massa é conduzido em um declive de a uma velocidade de quando acontece um defeito com suas rodas e elas travam. Ele passa então a deslizar sob a ação de uma força de atrito constante de que causa uma parada total do veículo.
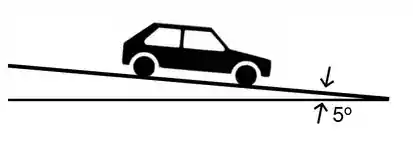
Dados: ; ; ;
Determine a aceleração do automóvel.
Determine o trabalho realizado pela força gravitacional.
Determine trabalho do atrito.
De acordo com seus resultados anteriores diga se foi possível confirmar, para a situação apresentada, a validade do teorema do trabalho e da energia cinética? Justifique.
Passo 1
Para determinar a aceleração precisamos lembrar da segunda lei de Newton:
Na situação do carro, por estarmos em um plano inclinado, iremos utilizar o plano como eixo , teremos então, nesse eixo:
Substituindo os valores dados, temos:
Passo 2
Para determinar o trabalho realizado pela força gravitacional, precisamos saber quanto o carro desce verticalmente, mas para isso precisamos saber o quanto ele percorre na ladeira, vamos então recorrer a cinemática! Usando Torricelli, temos:
Substituindo os valores dados, temos:
Agora que sabemos que o carro percorre , sabemos que ele descerá:
Agora podemos determinar o trabalho realizado pela força gravitacional:
Passo 3
Para determinar o trabalho realizado pela força de atrito, precisamos lembrara da fórmula:
Como já calculamos a distância percorrida pelo carro até ele parar, temos:
Passo 4
Relembrando o teorema do trabalho e da energia cinética, temos:
Para determinar a validade do teorema, vamos calcular cada termo separadamente, primeiro o trabalho total:
Agora podemos calcular a variação da energia cinética:
Podemos ver que o teorema é válido, pois temos:
Resposta