P3 de Física B - FIS1026 da PUCRIO - 2014.2

Assinale qual é a afirmativa verdadeira:

a) Para calcularmos o momento de inércia rotacional de um objeto em torno de um eixo, podemos considerar toda a sua massa concentrada no seu centro de massa.

b) O momento de inércia de um corpo rígido em torno de um eixo que passa pelo seu centro de massa é menor que o momento de inércia em torno de qualquer outro eixo paralelo.

c) Se a soma das forças em um objeto for zero, o torque neste objeto provocado por estas forças será zero também.

d) A energia cinética de um corpo girando em torno de um eixo depende somente da sua velocidade angular e da sua massa.

Um besouro encontra-se na borda de um disco muito leve que gira como um carrossel. Se o besouro se deslocar para o centro do disco, assinale qual é a afirmativa verdadeira em relação ao disco e ao sistema (disco + besouro):

a) A velocidade angular do disco aumenta e o momento de inércia do sistema aumenta.

b) A velocidade angular do disco diminui e o momento de inércia do sistema aumenta.

c) A velocidade angular do disco diminui e o momento de inércia do sistema diminui.

d) A velocidade angular do disco aumenta e o momento de inércia do sistema diminui.

Parte I:

Uma esfera sólida uniforme de massa e raio é colocada no lado de dentro de uma bacia hemisférica de raio . Existe atrito entre a esfera e a bacia. A esfera é liberada a partir do repouso fazendo um ângulo com a vertical, conforme ilustra a figura, e passa a rolar sem deslizar. A aceleração da gravidade é .

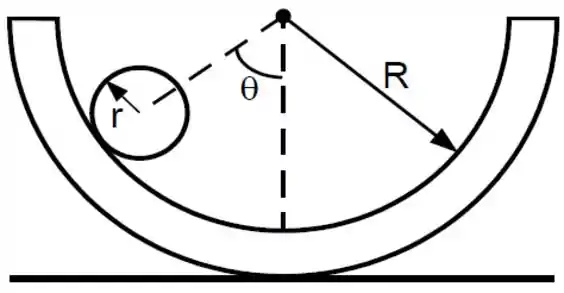
a) Expresse a conservação da energia do sistema.

b) Determine o módulo da velocidade angular da esfera quando ela atinge a parte inferior da bacia.

Parte II:

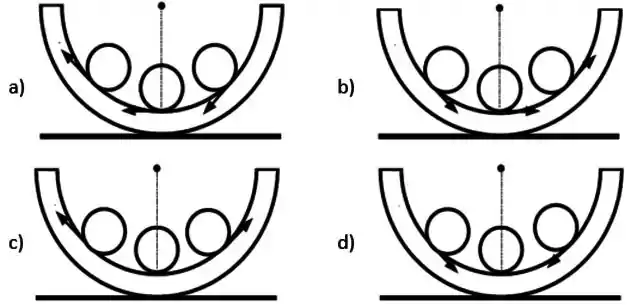
As setas no desenho abaixo, indicam as forças de atrito correspondentes à três posições da esfera quando ela está rolando sem deslizar no sentido horário. Assinale qual das opções é a verdadeira.

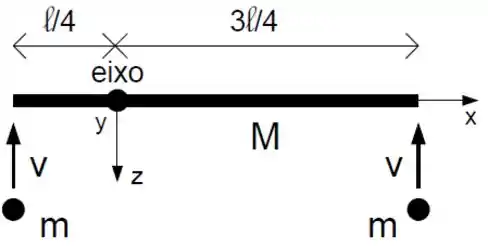
Na figura abaixo observa-se uma barra fina uniforme no plano horizontal de massa e comprimento . Ela está inicialmente em repouso e presa a um eixo fora do seu centro de massa que aponta na direção . Este eixo pode girar livremente. Duas partículas idênticas de massa se movimentam paralelamente com velocidade e vão se chocar simultaneamente com a barra nas suas extremidades, como mostra a figura. Após a colisão as partículas ficam grudadas na barra.

a) Calcule o momento de inércia da barra em relação ao eixo de rotação.

b) Calcule o momento angular do sistema logo antes da colisão em relação à origem.

c) Calcule a velocidade angular do sistema logo após a colisão.

Um objeto é composto por uma haste de massa desprezível e comprimento ligada ao centro de três discos de massa e raio como ilustra a figura. Este objeto está no plano vertical pode girar livremente em torno do eixo . No instante indicado na figura, a haste encontra-se inclinada de em relação ao eixo . O objeto está em equilíbrio estático, devido à força que tem direção perpendicular à haste. Despreze atritos. A aceleração da gravidade é .

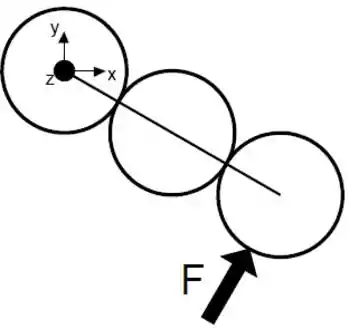
a) Calcule o torque produzido pela força e o torque produzido pela força da gravidade em termos dos dados do enunciado acima.

b) Suponha agora que , e . Em a força desaparece e o torque resultante é dado por . Calcule o módulo da aceleração angular para este instante e também para quando o objeto passar pela posição vertical.