Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões com Rotação

Ver Teoria
Exercício 111234567891012131415161718192021222324252627

Enunciado

Corpos Rígidos, Momento Angular

Na figura abaixo observa-se uma barra fina uniforme no plano horizontal x z de massa M = 1,0   k g e comprimento l = 1,0   m . Ela está inicialmente em repouso e presa a um eixo fora do seu centro de massa que aponta na direção y . Este eixo pode girar livremente. Duas partículas idênticas de massa m = M / 3 se movimentam paralelamente com velocidade v → = 10   m / s   - k → e vão se chocar simultaneamente com a barra nas suas extremidades, como mostra a figura. Após a colisão as partículas ficam grudadas na barra.

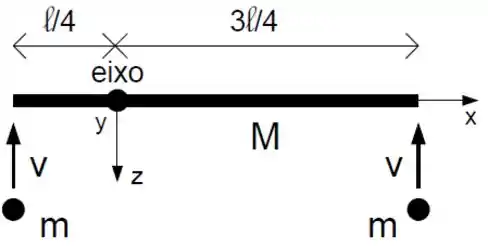
a) Calcule o momento de inércia da barra I e em relação ao eixo de rotação.

b) Calcule o momento angular do sistema logo antes da colisão L → A em relação à origem.

c) Calcule a velocidade angular ω → do sistema logo após a colisão.

Passo 1

a)

Temos uma barra uniforme de massa M e de comprimento l . Esse é um dos casos mais clássicos de questão de prova, não tem jeito, tem que saber o momento de inércia em relação ao eixo passando pelo centro de massa:

I c m = 1 12 M l 2

Passo 2

E ele pediu o momento de inércia em relação ao eixo de rotação, que é paralelo ao eixo que passa pelo CM. Então pelo teorema dos eixos paralelos:

I e = I c m + M d 2 ,

d sendo a distância entre os eixos.

O CM fica bem no meio da barra, a uma distância l 2 das extremidades, enquanto o eixo de rotação fica a l 4   m da ponta esquerda da barra. Assim, a distância entre os eixos é:

d = l 2 - l 4 = l 4

Passo 3

Então a fórmula do teorema dos eixos paralelos vai ficar assim:

I e = I c m + M d 2

⇒ I e = 1 12 M l 2 + M l 4 2

⇒ I e = 1 12 M l 2 + 1 16 M l 2 = 7 48 M l 2

Substituindo M = 1   k g   e l = 1   m , isso dá:

I e = 7 48 ≈ 0,146   k g ⋅ m 2

Passo 4

b)

A barra não tem momento angular, por estar em repouso. Portanto, o momento angular total do sistema L → A antes da colisão é a soma dos momentos angulares das 2 partículas.

O momento angular é dado por:

L → = r → × p → = r → × m v →

Então temos que achar os vetores posição r → , em relação à origem, das partículas da esquerda e da direita. Vou chamá-los de r → e s q e r → d i r , beleza?

Ambas as partículas tem massa m e velocidade v → , assim:

L → A = r → e s q × m v → + r → d i r × m v →

Passo 5

E logo antes da colisão, a gente tem:

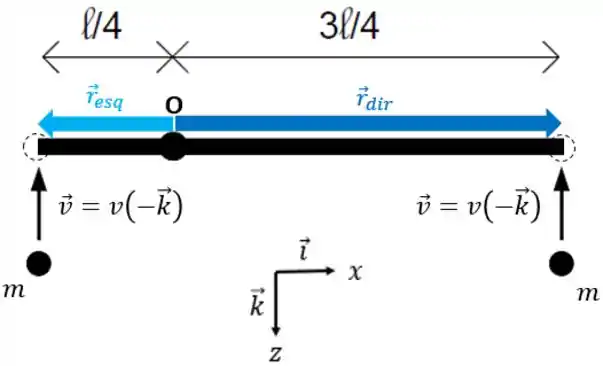
Dando uma espiada na figura aqui de cima, podemos ver que:

r → e s q = l 4 - i → r → d i r = 3 l 4 i →

Passo 6

Show, então o momento angular do sistema logo antes da colisão é:

L → A = r → e s q × m v → + r → d i r × m v →

⇒ L → A = l 4 - i → × m v - k → + 3 l 4 i → × m v - k →

⇒ L → A = m v l 4 - i → × - k → + 3 m v l 4 i → × - k →

E pela regra da mão direita:

- i → × - k → = - j →     e     i → × - k → = j →

Passo 7

Ou seja,

L → A = m v l 4 - j → + 3 m v l 4 j →

⇒ L → A = 3 m v l - m v l 4 j → = m v l 2 j →

Ele deu m = M 3 = 1 3   k g , v = 10   m / s e l = 1   m então:

L → A = 1 2 ∙ 1 3 ∙ 10 ∙ 1   j → = 10 6 j →

⇒ L → A = 5 3 j → ≈ 1,67   k g ⋅ m 2 / s   ( j → )  

Passo 8

c)

Agora ele quer a velocidade angular do sistema logo após a colisão.

Bem, acabamos de calcular o momento angular L → A do sistema logo antes da colisão, e tem uma fórmula que relaciona velocidade angular e momento angular:

L → = I ω →

Passo 9

Repare que não há torque externo agindo no nosso sistema, então o momento angular se conserva! Então, chamando o momento angular do sistema logo depois da colisão de L → D , temos:

L → A = L → D

Passo 10

Então sendo I D e ω → D o momento de inércia e a velocidade angular do sistema, respectivamente, logo depois da colisão, obtemos:

L → A = I D ω → D

⇒ 5 3 j → = I D ω → D

⇒ ω → D = 5 3 I D j →

E é justamente esse ω → D que ele pediu! Então precisamos achar o momento de inércia I D do sistema logo após a colisão.

Passo 11

Um detalhe bem importante é que as partículas ficam grudadas na barra, tipo assim:

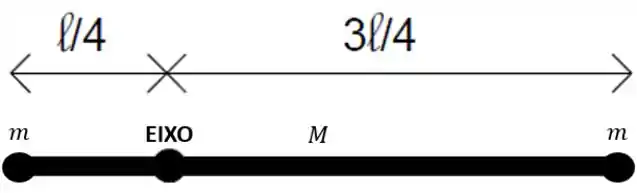
Então o I D que a gente tá procurando vai ser a soma dos momentos de inércia da barra, da partícula da esquerda e da partícula da direita, em relação ao eixo de rotação:

I D = I b a r r a + I e s q + I d i r

Passo 12

O momento de inércia da barra a gente já calculou lá na letra (a):

I b a r r a = 7 48 k g ⋅ m 2

E pra achar o momento de inércia das partículas, basta aplicar a fórmula

I = m r 2 ,

r sendo a distância da partícula ao eixo.

Ou seja,

I e s q = m l 4 2   e   I d i r = m 3 l 4 2

Passo 13

Juntando tudo:

I D = 7 48 + m l 4 2 + m 3 l 4 2

Substituindo m = M 3 = 1 3 e l = 1 , fica:

I D = 7 48 + 1 3 ∙ 1 16 + 1 3 ∙ 9 16

⇒ I D = 7 48 + 1 48 + 9 48 = 17 48   k g ⋅ m 2

Passo 14

Estamos quase acabando!

Lembrando que vimos antes:

ω → D = 5 3 I D j →

Ou seja,

ω → D = 5 3 ⋅ 17 48 j →

⇒ ω → D = 5 51 48 j →

⇒ ω → D = 5 ∙ 48 51 j → = 240 51 j → ≈ 4,71   r a d / s   ( j → )  

Resposta

a)

I e = 7 48 ≈ 0,146   k g ⋅ m 2

b)

L → A = 5 3 j → ≈ 1,67   k g ⋅ m 2 / s   j →

c)

ω → D = 240 51 j → ≈ 4,71   r a d / s   ( j → )

Exercícios de Livros Relacionados

Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Se, no sistema do Problema 64, L = 1,2m , M = 0,80k g , m = 0,30k g , e o maior ângulo entre a barra e a vertical após a colisão é 60 ° , determine a rapidez da partícula antes do impacto.
Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .