Assinale qual é a afirmativa verdadeira:
a) Para calcularmos o momento de inércia rotacional de um objeto em torno de um eixo, podemos considerar toda a sua massa concentrada no seu centro de massa.
b) O momento de inércia de um corpo rígido em torno de um eixo que passa pelo seu centro de massa é menor que o momento de inércia em torno de qualquer outro eixo paralelo.
c) Se a soma das forças em um objeto for zero, o torque neste objeto provocado por estas forças será zero também.
d) A energia cinética de um corpo girando em torno de um eixo depende somente da sua velocidade angular e da sua massa.
Passo 1
Alternativa (a):
Errado! Pra calcular o momento de inércia de um objeto, levamos em conta a distância de cada partícula que compõe o objeto ao eixo, então não podemos simplesmente considerar toda a massa concentrada!
Vamos parar pra olhar a fórmula do momento de inércia:
é a distância de cada pedacinho do objeto ao eixo. E essa distância pode variar de um pedacinho ao outro!
Então a alternativa (a) está errada.
Passo 2
Alternativa (b):
Pelo teorema dos eixos paralelos, o momento de inércia do corpo em relação a um eixo paralelo ao eixo que passa pelo centro de massa é:
sendo a distância entre os eixos.
E temos
portanto
Então a alternativa está correta.
Passo 3
Alternativa (c):
Pra provar que a alternativa está errada, basta achar um contraexemplo, e isso não vai ser muito difícil!
A soma das forças é zero, então podemos pegar duas forças de módulo igual e sentidos opostos. Pra alternativa estar errada, o torque não pode dar zero. Ele diz “o torque nesse objeto”, então assumimos que é o torque em relação ao centro de massa do objeto.
Qualquer coisa que gere rotação serve! Algo do tipo:
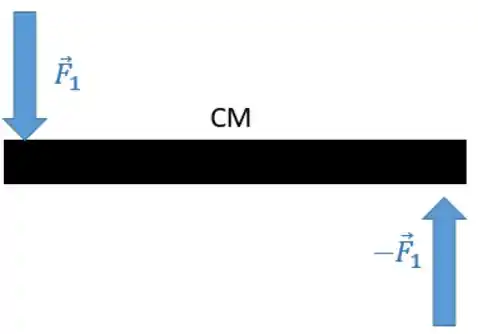
Se tiver um peso e uma normal se cancelando serve também! Contanto que a soma das forças dê zero e haja torque.
No exemplo da figura, temos . E claramente as forças realizam torque em relação a uma eixo passando pelo CM!
Portanto, a alternativa está errada.
Passo 4
Alternativa (d):
Vejamos, a energia cinética de rotação de um corpo girando em torno de um eixo é dada por:
Ou seja, ela depende da velocidade angular , que nem o enunciado disse, e do momento de inércia do corpo em relação ao eixo.
Mas não depende só do valor da massa! Que nem vimos pra alternativa (a), o momento de inércia depende de como essa massa é distribuída no corpo.
Portanto, a alternativa está errada.
Resposta
Alternativa (b)