P3 de Física B - FIS1026 da PUCRIO - 2015.1

Uma partícula de massa se move no plano com velocidade de módulo ao longo da direção dada pelo vetor . Calcule o momento angular da partícula em relação à origem do sistema de coordenadas em . Assinale a resposta correta.

(a)

(b)

(c)

(d)

(e) 0

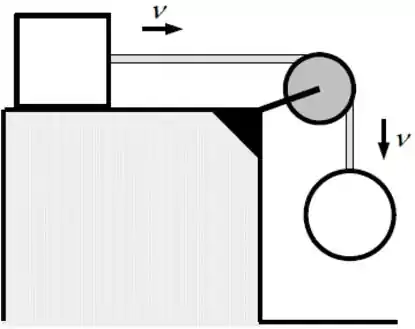
Uma esfera de massa 4,0 𝑘𝑔 e um cubo de massa 2,0 𝑘𝑔 estão conectados por uma corda inextensível e de massa de desprezível. A corda passa por uma roldana de raio 1,0 𝑚 e massa 2,0 𝑘𝑔 que tem a forma de um disco como ilustrado esquematicamente na figura ao lado. Ambos os corpos estão com velocidade de módulo igual a 𝑣 (𝑚/𝑠). Calcule em o módulo do momento angular do sistema em relação ao centro da roldana.

(a)

(b)

(c) 7

(d)

(e)

Na figura abaixo observa-se uma barra fina uniforme no plano horizontal de massa desprezível e comprimento . Ela está inicialmente em repouso e presa a um eixo que passa pelo seu centro de massa e aponta na direção . Este eixo pode girar livremente. Duas partículas de massa 𝑚 e 2𝑚 se movimentam paralelamente com velocidade 𝑣 na direção () e vão se chocar simultaneamente com a barra nas suas extremidades, como mostra a figura. Após a colisão as partículas ficam grudadas na barra.

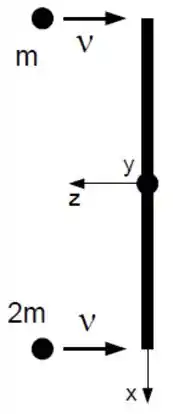
O módulo da velocidade angular do sistema logo após a colisão é igual a:

(a)

(b)

(c)

(d)

(e) 𝐴 𝑐𝑜𝑙𝑖𝑠ã𝑜 é 𝑡𝑜𝑡𝑎𝑙𝑚𝑒𝑛𝑡𝑒 𝑖𝑛𝑒𝑙á𝑠𝑡𝑖𝑐𝑎, 𝑝𝑜𝑟𝑡𝑎𝑛𝑡𝑜 𝑎 𝑣𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑𝑒 𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑎𝑝ó𝑠 𝑎 𝑐𝑜𝑙𝑖𝑠ã𝑜 é 𝑧𝑒𝑟𝑜.

No instante de tempo um objeto esférico de massa e raio , gira deslizando com velocidade angular e velocidade do centro de massa nula em uma superfície horizontal com coeficiente de atrito cinético (veja a figura). Considere como ponto de contato do objeto com a superfície a origem do sistema de coordenadas. Utilize para a aceleração da gravidade.

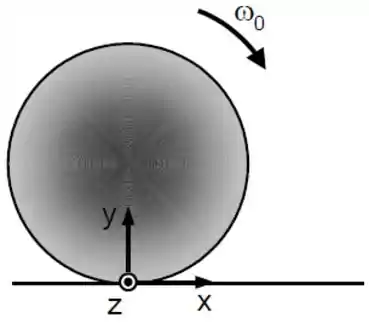
a) Faça um diagrama de corpo livre do objeto.

b) Escreva as equações de Newton que descrevem o movimento.

c) Determine, enquanto o objeto rola deslizando, aceleração do seu centro de massa e sua aceleração angular .

d) Escreva as expressões em função do tempo para a velocidade do centro de massa e para a velocidade angular 𝜔(𝑡) do objeto enquanto ele rola deslizando.

e) Sabendo que no tempo o objeto esférico passa a rolar sem deslizar, ache a razão entre suas energias cinéticas de translação e rotação.

Na preparação para um salto com vara, o atleta ilustrado abaixo mantém a vara em equilíbrio estático na posição horizontal. Para isto ele faz numa extremidade da vara, posição A, uma força na vertical para baixo igual a e na posição B uma força na vertical para cima igual a . A vara tem comprimento igual a 5,0 𝑚 e massa 3,0 𝑘𝑔.

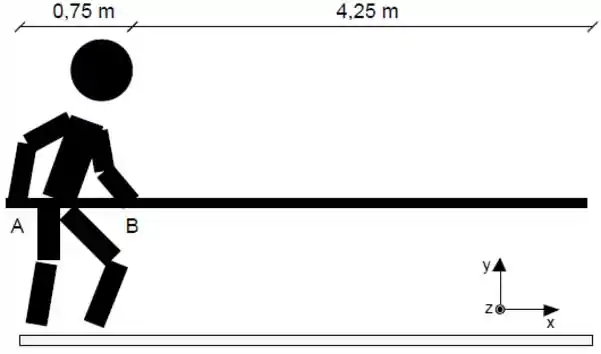
a) Calcule o momento de inércia rotacional da vara em relação ao eixo que passa pelo ponto B na direção do eixo .

b) Determine as forças e .

c) Suponha agora que em 𝑡 = 0 o atleta solte a vara na posição B e mantenha firme a posição A, de forma que a vara possa girar livremente em torno da posição A no plano em direção ao chão. Calcule o módulo da aceleração angular da barra neste instante.

d) Calcule a velocidade angular da barra quando o deslocamento angular for igual a .